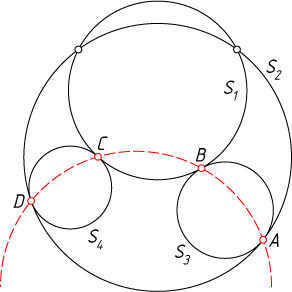
10607. Окружности S_{1}
и S_{2}
пересекаются в двух точках. Окружности S_{3}
и S_{4}
касаются окружности S_{1}
внешним образом в точках B
и C
соответственно, а окружности S_{2}
— внутренним образом в точках A
и D
соответственно (см. рисунок). Докажите, что точки A
, B
, C
и D
лежат на одной окружности.
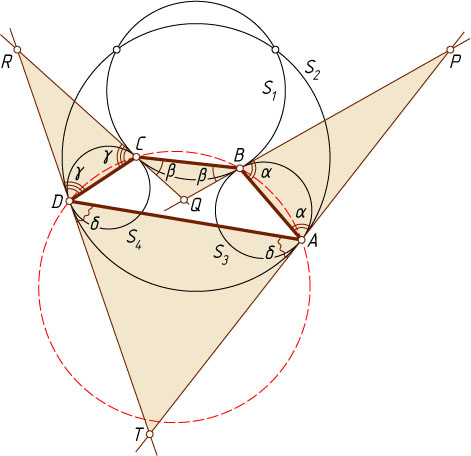
Решение. Пусть общая касательная к окружностям S_{2}
и S_{3}
в точке A
и общая касательная к окружностям S_{2}
и S_{4}
в точке D
пересекаются в точке T
. Аналогично, P
, Q
и R
— точки пересечения общих касательных трёх остальных пар данных окружностей (см. рис.).
Обозначим через \alpha
, \beta
, \gamma
и \delta
углы при основаниях AB
, BC
, CD
и AD
равнобедренных треугольников ABP
, BQC
, CDR
и ADT
. Тогда
\angle BAD=180^{\circ}-\alpha-\delta,~\angle ABC=180^{\circ}-\alpha+\beta,
\angle BCD=180^{\circ}-\gamma+\beta,~\angle ADC=180^{\circ}-\gamma-\delta.
Значит,
\angle BAD+\angle BCD=(180^{\circ}-\alpha-\delta)+(180^{\circ}-\gamma+\beta)=
=(180^{\circ}-\alpha+\beta)+(180^{\circ}-\gamma-\delta)=\angle ABC+\angle ADC.
Следовательно,
\angle BAD+\angle BCD=\angle ABC+\angle ADC=180^{\circ},
т. е. четырёхугольник ABCD
вписанный.
Источник: Саратовская олимпиада. — 1981/1982, III тур, 10 класс
Источник: Андреева А. Н., Барабанов А. И., Чернявский И. Я. Саратовские математические олимпиады. 1950/51—1994/95. — М.: МЦНМО, 2013. — № 781, с. 80

