1061. Через середину Q
отрезка MN
, концы которого лежат на боковых сторонах равнобедренного треугольника, проведена прямая, параллельная основанию треугольника и пересекающая боковые стороны в точках K
и L
. Докажите, что проекция отрезка MN
на основание треугольника равна отрезку KL
.
Указание. Докажите, что MK=NL
.
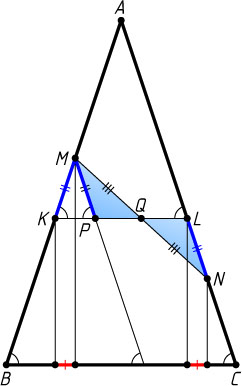
Решение. Пусть точки M
и K
лежат на стороне AB
равнобедренного треугольника ABC
(AB=AC)
, а точки N
и L
— на его стороне AC
. Если MN\parallel BC
, то утверждение очевидно.
Пусть AM\lt AN
. Через точку M
проведём прямую, параллельную AC
, до пересечения в точке P
с прямой KL
. Если Q
— середина MN
, то из равенства треугольников PQM
и LQN
следует, что PM=NL
.
С другой стороны, поскольку
\angle PKM=\angle AKL=\angle ALK=\angle MPK,
то треугольник MPK
— равнобедренный. Поэтому MK=MP=NL
.
Итак, отрезки MK
и NL
равны и образуют с прямой BC
равные углы. Поэтому их проекции на BC
равны между собой. Следовательно, проекции отрезков KL
и MN
на BC
также равны между собой.
Источник: Польские математические олимпиады. — 1956, задача 5
Источник: Страшевич С., Бровкин Е. Польские математические олимпиады. — М.: Мир, 1978. — № 47, с. 17
