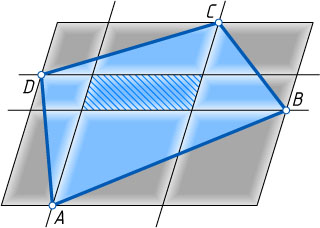
10610. Параллелограмм двумя парами прямых, параллельных его сторонам, разбивается на девять параллелограммов (см. рис.). Найдите площадь четырёхугольника ABCD
, если площадь исходного параллелограмма равна S
, а площадь внутреннего (заштрихованного) параллелограмма равна s
.
Ответ. \frac{S+s}{2}
.
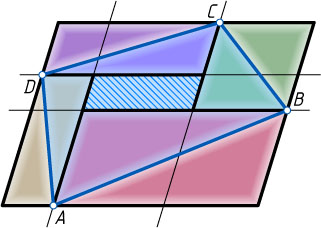
Решение. Площадь четырёхугольника ABCD
равна разности площади исходного параллелограмма и суммы половин площадей восьми из девяти (без внутреннего) параллелограммов разбиения, т. е.
S_{ABCD}=S-\frac{S-s}{2}=\frac{S+s}{2}.
Источник: Саратовская олимпиада. — 1988/1989, III тур, 8 класс
Источник: Андреева А. Н., Барабанов А. И., Чернявский И. Я. Саратовские математические олимпиады. 1950/51—1994/95. — М.: МЦНМО, 2013. — № 987, с. 101

