10615. Точки K
, L
и M
лежат на сторонах соответственно BC
, AC
и AB
правильного треугольника ABC
. Отрезки AK
, BL
и CM
разбивают треугольник ABC
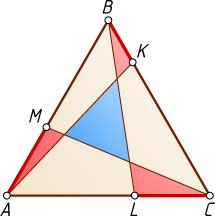
на четыре треугольника и три четырёхугольника (см. рис.). Известно, что площадь внутреннего треугольника равна сумме площадей трёх остальных треугольников разбиения. Докажите, что AM+BK+CL=AB
.
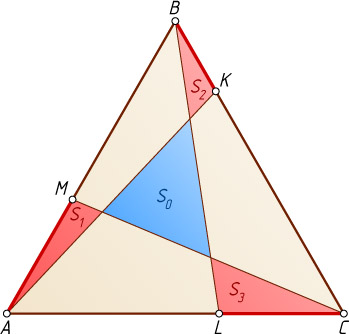
Решение. Пусть площадь равностороннего треугольника ABC
равна S
, его высота равна h
, площадь внутреннего треугольника равна S_{0}
, а площади треугольников разбиения со сторонами AM
, BK
и CL
равны S_{1}
, S_{2}
и S_{3}
соответственно. Тогда
S_{0}=S-S_{\triangle AMC}-S_{\triangle AKB}-S_{\triangle BLC}+S_{1}+S_{2}+S_{3},
а так как
S_{1}+S_{2}+S_{3}=S_{0},
то
S_{\triangle AMC}+S_{\triangle AKB}+S_{\triangle BLC}=S,
или
\frac{1}{2}AM\cdot h+\frac{1}{2}BK\cdot h+\frac{1}{2}CL\cdot h=\frac{1}{2}AB\cdot h.
Отсюда следует, что
AM+BK+CL=AB.
Источник: Саратовская олимпиада. — 1990/1991, III тур, 10 класс
Источник: Андреева А. Н., Барабанов А. И., Чернявский И. Я. Саратовские математические олимпиады. 1950/51—1994/95. — М.: МЦНМО, 2013. — № 1072, с. 111

