10643. Перпендикуляры, восставленные к сторонам AB
и CD
вписанного четырёхугольника ABCD
в точках B
и D
, пересекают прямые CD
и AB
в точках B'
и D'
соответственно. Докажите, что AC\parallel B'D'
.
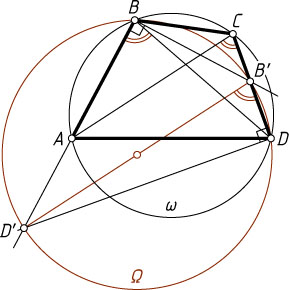
Решение. Рассмотрим случай, изображённый на рисунке.
Пусть четырёхугольник ABCD
вписан в окружность \omega
. Из точек B
и D
отрезок B'D'
виден под прямым углом, значит, эти точки лежат на окружности \Omega
с диаметром B'D'
. Вписанные в окружность \Omega
углы DB'D'
и DBD'
опираются на одну и ту же дугу, поэтому
\angle DB'D'=\angle DBD'=\angle DBA.
Вписанные в окружность \omega
углы DBA
и DCA
также опираются на одну и ту же дугу, поэтому
\angle DBA=\angle DCA.
Значит,
\angle DB'D'=\angle DCA.
Следовательно, B'D'\parallel AC
.
Аналогично для любого другого случая.
Источник: Posamentier A. S., Salkind Ch. T. Challenging Problems in Geometry. — N.Y.: Dover Publication, 2017. — № 4.34, с. 22
