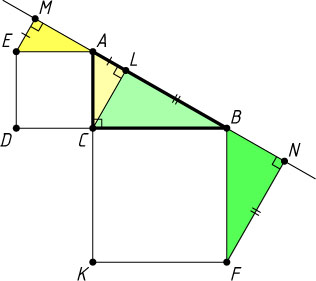
1065. На катетах AC
и BC
прямоугольного треугольника вне его построены квадраты ACDE
и BCKF
. Из точек E
и F
на продолжение гипотенузы опущены перпендикуляры EM
и FN
. Докажите, что
EM+FN=AB.
Указание. Опустите перпендикуляр из вершины C
на гипотенузу AB
.
Решение. Пусть CL
— высота прямоугольного треугольника ABC
. Тогда прямоугольный треугольник AME
равен прямоугольному треугольнику CLA
, а прямоугольный треугольник BNF
— прямоугольному треугольнику CLB
. Поэтому EM=AL
и FN=BL
. Следовательно,
EM+FN=AL+BL=AB.
Источник: Журнал «Квант». — 1975, № 10, с. 48, задача 11
