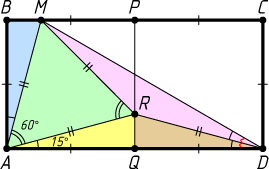
1068. В прямоугольнике ABCD
стороны AB
и CD
вдвое короче сторон BC
и AD
. На стороне BC
выбрана точка M
, для которой \angle MAB=15^{\circ}
. Найдите угол MDA
.
Ответ. 30^{\circ}
.
Указание. Докажите, что треугольник ADM
равнобедренный. Для этого на отрезке, соединяющем середины сторон BC
и AD
, отметьте точку R
, для которой \angle ADR=15^{\circ}
.
Решение. Первый способ. Пусть P
и Q
середины сторон BC
и AD
соответственно, R
— точка на отрезке PQ
, для которой \angle ADR=15^{\circ}
. Тогда
\angle RAQ=\angle QDR=\angle MAB=15^{\circ},~\angle MAR=90^{\circ}-15^{\circ}-15^{\circ}=60^{\circ},
а так как AQ=\frac{1}{2}AD=AB
, то прямоугольные треугольники AQR
и ABM
равны по катету и прилежащему острому углу, поэтому AM=AR
. Значит, треугольник AMR
— равносторонний. Следовательно, \angle ARM=60^{\circ}
и DR=AR=MR
.
Из равнобедренного треугольника ARD
находим, что \angle ARD=150^{\circ}
, поэтому
\angle DRM=360^{\circ}-60^{\circ}-150^{\circ}=150^{\circ}.
Значит, треугольники ARD
и MRD
равны по двум сторонам и углу между ними. Следовательно, MD=AD
.
Из равнобедренного треугольника ADM
находим, что
\angle MDA=180^{\circ}-2\angle MAD=180^{\circ}-2(90^{\circ}-15^{\circ})=180^{\circ}-150^{\circ}=30^{\circ}.
Второй способ. Положим AB=CD=x
, BC=AD=2x
. Поскольку
\tg15^{\circ}=\tg(45^{\circ}-30^{\circ})=\frac{\tg45^{\circ}-\tg30^{\circ}}{1+\tg45^{\circ}\tg30^{\circ}}=\frac{1-\frac{1}{\sqrt{3}}}{1+\frac{1}{\sqrt{3}}}=2-\sqrt{3},
из прямоугольного треугольника ABM
находим, что
BM=AB\tg15^{\circ}=x(2-\sqrt{3}).
Тогда
MC=BC-BM=2x-x(2-\sqrt{3})=x\sqrt{3}.
Из прямоугольного треугольника DCM
получаем
\tg\angle CDM=\frac{MC}{CD}=\frac{x\sqrt{3}}{x}=\sqrt{3}.
Значит, \angle DCM=60^{\circ}
. Следовательно, \angle MDA=30^{\circ}
.
Третий способ. От луча DA
в полуплоскость, содержащую точку C
, отложим луч под углом 30^{\circ}
к лучу DA
. Пусть отложенный луч пересекает прямую BC
в точке M'
, а AH
— высота треугольника ADM'
. Тогда прямоугольные треугольники ABM'
и AHM'
равны по катету и гипотенузе. Значит, AM'
— биссектриса угла BAH
, равного
90^{\circ}-\angle DAH=90^{\circ}-60^{\circ}=30^{\circ}.
Тогда \angle BAM'=15^{\circ}=\angle BAM
, поэтому точка M'
совпадает с M
. Следовательно, \angle MDA=30^{\circ}
.