10686. Точки D
, E
и F
лежат на сторонах соответственно BC
, CA
и AB
треугольника ABC
. Окружности, вписанные в треугольники AEF
, BFD
и CDE
, имеют один и тот же радиус r
. Пусть r_{1}
и r_{2}
— радиусы окружностей, вписанных в треугольники DEF
и ABC
соответственно. Докажите, что r+r_{1}=r_{2}
.
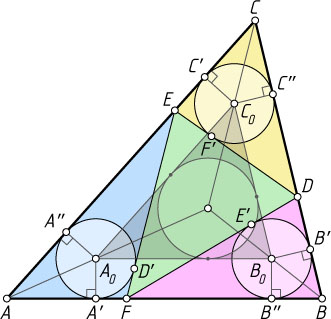
Решение. Введём обозначения, как показано на рисунке. Тогда
DE+EF+FD=(DF'+F'E)+(ED'+D'F)+(FE'+E'D)=
=(DC''+C'E)+(EA''+A'F)+(FB''+B'D)=
=(DC''+B'D)+(EA''+C'E)+(FB''+A'F)=
=B'C''+C'A''+A'B''=B_{0}C_{0}+C_{0}A_{0}+A_{0}B_{0}.
Кроме того,
S_{\triangle DCE}+S_{\triangle EAF}+S_{\triangle BEF}=
=\frac{1}{2}r(CD+DE+CE)+\frac{r}{2}(AF+FE+EA)+\frac{r}{2}(BD+DF+FB)=
=\frac{r}{2}((BD+CD)+(AF+FB)+(CE+EA)+(DE+FE+DF))=
=\frac{r}{2}(BC+AB+CA+DE+FE+DF),
поэтому
S_{\triangle DEF}=S_{\triangle ABC}-(S_{\triangle DCE}+S_{\triangle EAF}+S_{\triangle BEF})=
=S_{\triangle ABC}-\frac{r}{2}(BC+AB+CA+DE+EF+FD),
а так как
S_{\triangle A_{0}B_{0}C_{0}}=S_{\triangle ABC}-(S_{BCC_{0}B_{0}}+S_{CAA_{0}C_{0}}+S_{ABB_{0}A_{0}})=
=S_{\triangle ABC}-\left(\frac{BC+C_{0}B_{0}}{2}\cdot r+\frac{CA+A_{0}C_{0}}{2}\cdot r+\frac{AB+B_{0}A_{0}}{2}\cdot r\right)=
=S_{\triangle ABC}-\frac{r}{2}(BC+C_{0}B_{0}+CA+A_{0}C_{0}+AB+B_{0}A_{0})=
=S_{\triangle ABC}-\frac{r}{2}((BC+CA+AB)+(B_{0}C_{0}+C_{0}A_{0}+A_{0}B_{0}))=
=S_{\triangle ABC}-\frac{r}{2}((BC+CA+AB)+(DE+EF+FD)),
то S_{\triangle A_{0}B_{0}C_{0}}=S_{\triangle DEF}
.
Таким образом, периметры и площади треугольников DEF
и A_{0}B_{0}C_{0}
равны. Значит, равны радиусы их вписанных окружностей, и радиус вписанной окружности треугольника A_{0}B_{0}C_{0}
тоже равен r_{1}
.
Лучи AA_{0}
и BB_{0}
(т. е. биссектрисы углов BAC
и ABC
) пересекаются в центре вписанной окружности треугольника ABC
, поэтому радиус вписанной окружности треугольника A_{0}B_{0}C_{0}
равен r_{2}-r
. Из равенства r_{2}-r=r_{1}
получаем, что r+r_{1}=r_{2}
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1988, № 2, задача 1191 (1986, с. 28), с. 55
