10710. Две окружности касаются внутренним образом в точке A
. Точки P
и Q
лежат на большей окружности, M
и N
— точки пересечения отрезка PQ
с меньшей окружностью. Докажите, что \angle PAM=\angle NAQ
.
Решение. Пусть точка M
лежит между P
и N
. Через точку A
проведём общую касательную к окружностям. Отметим на ней такую точку B
, чтобы точки B
и Q
лежали по разные стороны от прямой AP
. Продолжим отрезки AM
и AN
до пересечения с большей окружностью в точках M_{1}
и N_{1}
соответственно. Из теоремы об угле между касательной и хордой следует, что
\angle AN_{1}M_{1}=\angle BAM_{1}=\angle BAM=\angle ANM.
Значит, MN\parallel M_{1}N_{1}
, т. е. PQ
и M_{1}N_{1}
— параллельные хорды большей окружности. Дуги, заключённые между параллельными хордами, равны. Следовательно, равны и опирающиеся на них вписанные углы, т. е.
\angle PAM=\angle PAM_{1}=\angle N_{1}AQ=\angle NAQ.
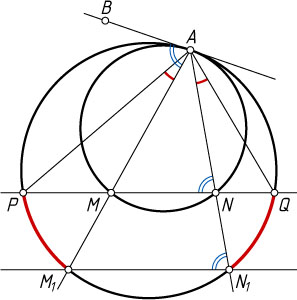
Источник: Кушнир И. А. Геометрия. Поиск и вдохновение. — М.: МЦНМО, 2013. — с. 265
