1074. Найдите геометрическое место середин отрезков, у которых один конец лежит на одной данной окружности, а другой — на другой данной окружности.
Ответ. Кольцо, ограниченное двумя концентрическими окружностями, или круг.
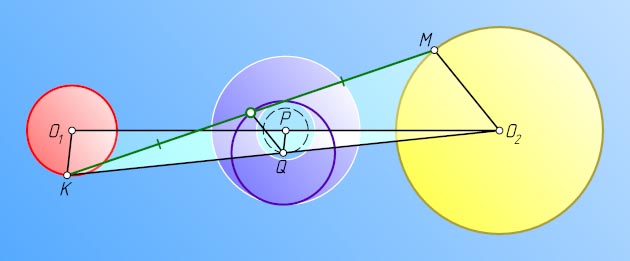
Решение. Пусть r_{1}
и r_{2}
— радиусы окружностей с центрами O_{1}
и O_{2}
соответственно. Зафиксируем точку K
первой окружности и найдём геометрическое место середин отрезков KM
, где точка M
пробегает вторую окружность.
При гомотетии с центром K
и коэффициентом \frac{1}{2}
центр O_{2}
второй окружности переходит в середину Q
отрезка KO_{2}
, а окружность с центром O_{2}
в окружность радиуса \frac{r_{2}}{2}
с центром Q
. При этом, если P
— середина отрезка O_{1}O_{2}
, то PQ
— средняя линия треугольника O_{1}KO_{2}
, поэтому PQ=\frac{1}{2}O_{1}K=\frac{r_{1}}{2}
. Значит, для любой точки K
точка Q
лежит на расстоянии \frac{r_{1}}{2}
от фиксированной точки P
, т. е. на окружности с центром P
и радиусом \frac{r_{1}}{2}
. Таким образом, искомое геометрическое место есть объединение всех окружностей радиуса \frac{r_{2}}{2}
с центрами, лежащими на окружности радиуса \frac{r_{1}}{2}
с центром P
.
Если r_{1}\ne r_{2}
, то получим кольцо между окружностями с центром P
радиусов \frac{r_{1}}{2}+\frac{r_{2}}{2}
и \left|\frac{r_{2}}{2}-\frac{r_{1}}{2}\right|
. Если же r_{1}=r_{2}
, получим круг.
Источник: Васильев Н. Б., Гутенмахер В. Л. Прямые и кривые. — 2-е изд. — М.: Наука, 1978. — № 3.20(б), с. 46
