10740. Точки L
, E
, F
и K
— середины сторон выпуклого четырёхугольника ABCD
(см. рис.). Отрезок AE
пересекает отрезки DL
и BF
в точках M
и N
соответственно, отрезок CK
пересекает отрезки BF
и DL
в точках P
и Q
соответственно. Докажите, что сумма площадей треугольников ALM
, BEN
, CFP
и DKQ
равна площади четырёхугольника MNPQ
.
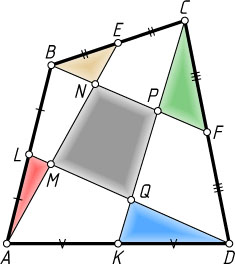
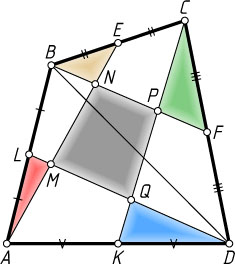
Решение. Пусть площадь четырёхугольника ABCD
равна S
. Проведём диагональ BD
. Отрезок DL
— медиана треугольника ABD
, поэтому S_{\triangle ADL}=\frac{1}{2}S_{\triangle ABD}
. Аналогично S_{\triangle BCF}=\frac{1}{2}S_{\triangle BCD}
. Значит,
S_{\triangle ADL}+S_{\triangle BCF}=\frac{1}{2}S_{\triangle ABD}+\frac{1}{2}S_{\triangle BCD}=\frac{1}{2}S_{ABCD}=\frac{1}{2}S.
Аналогично S_{\triangle ABE}+S_{\triangle CDK}=\frac{1}{2}S
, поэтому
S_{\triangle ADL}+S_{\triangle BCF}+S_{\triangle ABE}+S_{\triangle CDK}=S.
Следовательно,
S_{MNPQ}=S-(S_{\triangle ADL}+S_{\triangle BCF}+S_{\triangle ABE}+S_{\triangle CDK})+
+S_{\triangle ALM}+S_{\triangle BEN}+S_{\triangle CFP}+S_{\triangle DKQ}=
=S-S+S_{\triangle ALM}+S_{\triangle BEN}+S_{\triangle CFP}+S_{\triangle DKQ}=
=S_{\triangle ALM}+S_{\triangle BEN}+S_{\triangle CFP}+S_{\triangle DKQ}.
