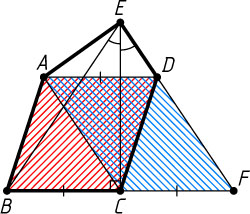
1075. В выпуклом пятиугольнике ABCDE
стороны AB
и CD
равны и параллельны, сторона DE
параллельна диагонали AC
, а угол BCE
прямой. Докажите, что EC
— биссектриса угла BED
.
Указание. Продолжите ED
до пересечения с BC
.
Решение. Противоположные стороны AB
и CD
четырёхугольника ABCD
равны и параллельны, значит, это параллелограмм. Поэтому BC\parallel AD
и BC=AD
. Продолжим отрезки BC
и ED
до пересечения в точке F
. Противоположные стороны четырёхугольника ACFD
попарно параллельны, значит, ACFD
— также параллелограмм, поэтому CF=AD
. Следовательно, CF=BC
, т. е. C
— середина отрезка BF
.
Прямая CE
перпендикулярна отрезку BF
и проходит через его середину, значит, CE
— серединный перпендикуляр к отрезку BF
. Следовательно, EC
— биссектриса угла BEF
, а значит, угла BED
.