1076. На стороне BC
квадрата ABCD
отмечены точки K
и L
, причём BK=KL=LC
. На стороне AD
отмечена точка M
, причём AM=\frac{1}{3}AD
. Найдите сумму углов, под которыми виден отрезок AM
из точек K
, L
и C
.
Ответ. 45^{\circ}
.
Указание. Отметьте середину отрезка MD
и рассмотрите равные прямоугольные треугольники.
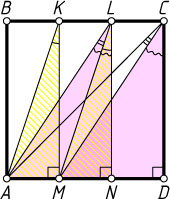
Решение. Пусть N
— середина отрезка MD
. Тогда прямоугольные треугольники MLN
и AKM
равны по двум катетам. Аналогично равны прямоугольные треугольники MCD
и ALN
. Следовательно,
\angle AKM+\angle ALM=\angle MLN+\angle ALM=\angle ALN=\angle MCD,
\angle AKM+\angle ALM+\angle ACM=\angle MCD+\angle ACM=\angle ACD=45^{\circ}.
Источник: Шень А. Х. Геометрия в задачах. — М.: МЦНМО, 2013. — № 246, с. 75
