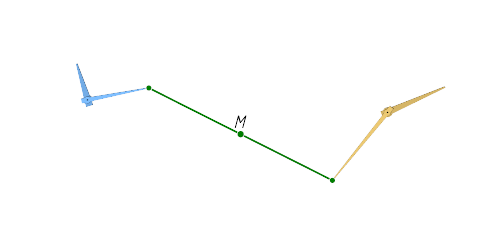
1078. На столе лежат двое плоских часов. И те, и другие идут точно, но не обязательно показывают одинаковое время. По какой линии движется середина M
отрезка, соединяющего концы их минутных стрелок?
 <
<

Ответ. По окружности с центром в середине отрезка с концами в центрах часов.
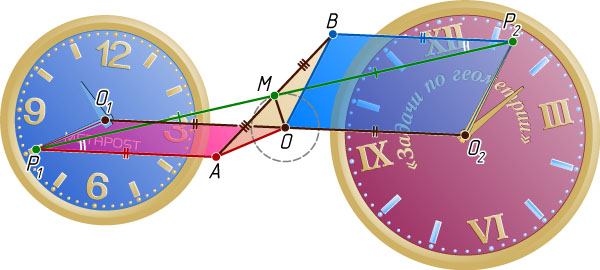
Решение. Пусть O_{1}
и O_{2}
— центры часов, P_{1}
и P_{2}
соответственно — концы минутных стрелок, O
и M
— середины отрезков O_{1}O_{2}
и P_{1}P_{2}
соответственно.
Рассмотрим параллелограммы P_{1}O_{1}OA
и P_{2}O_{2}OB
. Из равенства треугольников MP_{2}B
и MP_{1}A
(по двум сторонам и углу между ними) следует равенство углов BMP_{2}
и AMP_{1}
, поэтому точки A
, M
и B
лежат на одной прямой, причём M
— середина отрезка AB
.
Стороны OA
и OB
треугольника AOB
соответственно равны и параллельны отрезкам O_{1}P_{1}
и O_{2}P_{2}
. Эти отрезки с одинаковой угловой скоростью (1 оборот в час) вращаются вокруг точек O_{1}
и O_{2}
, значит, медиана OM
треугольника AOB
вращается с той же угловой скоростью вокруг точки O
. Следовательно, точка M
движется по фиксированной окружности с центром O
и радиусом, равным медиане OM
.
Источник: Васильев Н. Б., Гутенмахер В. Л. Прямые и кривые. — 2-е изд. — М.: Наука, 1978. — № 1.28, с. 22
 <
<

