1079. Точки X
и Y
— середины диагоналей соответственно AC
и BD
выпуклого четырёхугольника ABCD
. Прямые BC
и AD
пересекаются в точке P
. Докажите, что площадь треугольника PXY
в четыре раза меньше площади четырёхугольника ABCD
.
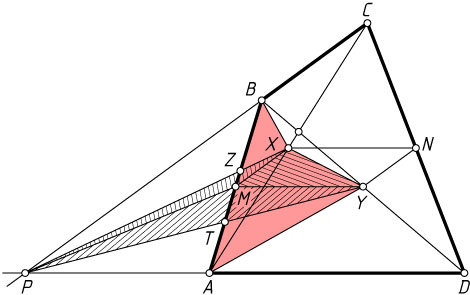
Решение. Первый способ. Пусть M
и N
— середины сторон AB
и CD
соответственно, а точка P
и сторона CD
лежат по разные стороны от прямой AB
. Четырёхугольник MXNY
— параллелограмм, поэтому S_{\triangle MXY}=S_{\triangle NXY}
.
Обозначим S_{ABCD}=S
. Тогда
S_{\triangle ACD}+S_{\triangle ABD}+S_{\triangle ABC}+S_{\triangle BCD}=2S.
Отрезок MX
— средняя линия треугольника ABC
, поэтому прямые MX
и CP
параллельны, значит, точки B
и P
равноудалены от прямой MX
. Следовательно,
S_{\triangle PMX}=S_{\triangle BMX}=S_{BCXM}-S_{\triangle BCX}=
=\frac{3}{4}S_{\triangle ABC}-\frac{1}{2}S_{\triangle ABC}=\frac{1}{4}S_{\triangle ABC}.
Аналогично точки A
и P
также равноудалены от прямой MY
. Следовательно,
S_{\triangle PMY}=S_{\triangle AMY}=\frac{1}{4}S_{\triangle ABD}.
Кроме того, точка Z
пересечения диагоналей BM
и PX
трапеции BPMX
лежит внутри трапеции BPMX
, а точка T
пересечения диагоналей трапеции AYMP
— внутри трапеции AYMP
, поэтому точка M
лежит на отрезке ZT
, а значит, внутри треугольника PXY
.
Заметим, что
S_{MXNY}=S-S_{\triangle CNX}-S_{\triangle DNY}-S_{AMYD}-S_{BCXM}=S-\frac{1}{4}S_{\triangle ACD}-\frac{1}{4}S_{\triangle BCD}-\frac{3}{4}S_{\triangle ABD}-\frac{3}{4}S_{\triangle ABC}.
Следовательно,
S_{\triangle PXY}=S_{\triangle MXY}+S_{\triangle PMX}+S_{\triangle PMY}=\frac{1}{2}S_{MXNY}+S_{\triangle PMX}+S_{\triangle PMY}=
=\frac{1}{2}\left(S-\frac{1}{4}S_{\triangle ACD}-\frac{1}{4}S_{\triangle BCD}-\frac{3}{4}S_{\triangle ABD}-\frac{3}{4}S_{\triangle ABC}\right)+\frac{1}{4}S_{\triangle ABC}+\frac{1}{4}S_{\triangle ABD}=
=\frac{1}{2}S-\frac{1}{8}\left(S_{\triangle ACD}+S_{\triangle ABD}+S_{\triangle ABC}+S_{\triangle BCD}\right)=\frac{1}{2}S-\frac{1}{8}\cdot2S=\frac{1}{4}S.
Что и требовалось доказать.
Второй способ. Пусть M
— середина стороны AB
, а точка P
и сторона CD
лежат по разные стороны от прямой AB
. Отрезок MX
— средняя линия треугольника ABC
, поэтому MX\parallel CP
. Аналогично MY\parallel DP
. Точка Z
пересечения диагоналей BM
и PX
трапеции BPMX
лежит внутри трапеции BPMX
, а точка T
пересечения диагоналей трапеции APMY
— внутри трапеции APMY
, поэтому точка M
лежит на отрезке ZT
, а значит, внутри треугольника PXY
.
Треугольник PMX
равновелик треугольнику BMX
, а треугольник PMY
— треугольнику AMY
, значит, треугольник PXY
равновелик четырёхугольнику ABXY
, диагонали AX
и BY
которого равны половинам диагоналей AC
и BD
четырёхугольника ABCD
. Поскольку площадь любого четырёхугольника равна половине произведения диагоналей на синус угла \varphi
между ними, то
S_{\triangle PXY}=S_{ABXY}=\frac{1}{2}AX\cdot BY\sin\varphi=\frac{1}{2}\cdot\frac{1}{2}AC\cdot\frac{1}{2}BD\sin\varphi=\frac{1}{4}\cdot\frac{1}{2}AC\cdot BD\sin\varphi=\frac{1}{4}S_{ABCD}.
Что и требовалось доказать.
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 69
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — задача 1, с. 91
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.29б, с. 85
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 4.29б, с. 86
