1082. На сторонах треугольника ABC
внешним образом построены подобные треугольники AC_{1}B
, ACB_{1}
и A_{1}BC
. Докажите, что центры их описанных окружностей являются вершинами треугольника, подобного трём построенным. (Углы при вершинах A_{1}
, B_{1}
, C_{1}
построенных треугольников не являются соответственными.)
Указание. Сумма углов при вершинах A_{1}
, B_{1}
и C_{1}
построенных треугольников равна 180^{\circ}
, поэтому их описанные окружности пересекаются в одной точке.
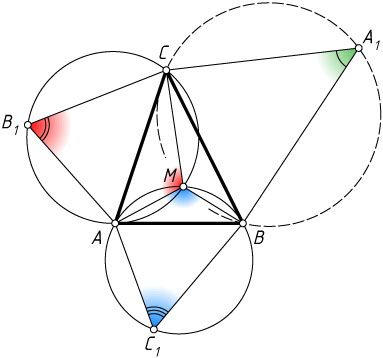
Решение. Лемма. Если на сторонах треугольника ABC
внешним образом построены подобные треугольники AC_{1}B
, ACB_{1}
и A_{1}BC
(рис. 1), то описанные окружности построенных треугольников пересекаются в одной точке.
Доказательство. Обозначим через M
точку пересечения окружностей, описанных около треугольников AC_{1}B
и ACB_{1}
, отличную от A
, и докажем, что точка M
лежит на окружности, описанной около треугольника A_{1}BC
.
Поскольку углы при вершинах A_{1}
, B_{1}
, C_{1}
построенных треугольников не являются соответственными, их сумма равна 180^{\circ}
.
Пусть точка лежит внутри треугольника ABC
. Тогда
\angle BMC=360^{\circ}-\angle AMB-\angle AMC=
=360^{\circ}-(180^{\circ}-\angle AC_{1}B)-(180^{\circ}-\angle AB_{1}C)=\angle AC_{1}B+\angle AB_{1}C,
поэтому
\angle BMC+\angle BA_{1}C=\angle AC_{1}B+\angle AB_{1}C+\angle BA_{1}C=180^{\circ}.
Следовательно, точки B
, A_{1}
, M
, C
лежат на одной окружности, т. е. все три окружности проходят через точку M
. Аналогично для остальных случаев. Лемма доказана.
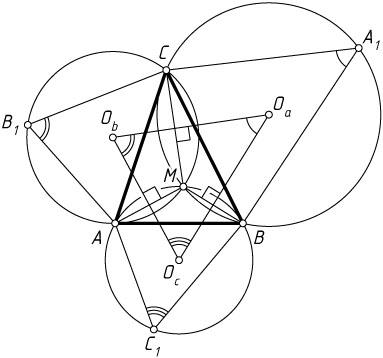
Перейдём к нашей задаче (рис. 2). Пусть O_{c}
, O_{b}
и O_{a}
— центры описанных окружностей треугольников AC_{1}B
, ACB_{1}
и A_{1}BC
соответственно. По доказанной лемме эти окружности имеют общую точку M
. Линия центров пересекающихся окружностей перпендикулярна их общей хорде, значит, O_{a}O_{c}\perp BM
и O_{a}O_{b}\perp CM
. Поэтому
\angle O_{b}O_{a}O_{c}=180^{\circ}-\angle BMC=\angle BA_{1}C.
Аналогично \angle O_{a}O_{b}O_{c}=\angle AB_{1}C=\angle CBA_{1}
. Следовательно, треугольник O_{a}O_{b}O_{c}
подобен треугольнику A_{1}BC
по двум углам. Что и требовалось доказать.
Примечание. Из доказанного утверждения следует, что если на сторонах произвольного треугольника построить внешним (или внутренним) образом равносторонние треугольники, то их центры будут вершинами равностороннего треугольника (треугольник Наполеона).
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 78

