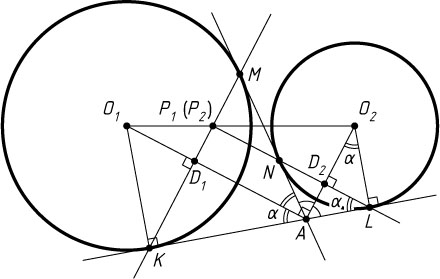
1083. К двум окружностям, расположенным одна вне другой, проведены одна внешняя и одна внутренняя общие касательные. Рассмотрим две прямые, каждая из которых проходит через точки касания, принадлежащие одной из окружностей. Докажите, что точка пересечения этих прямых расположена на прямой, проходящей через центры окружностей.
Решение. Пусть внешняя касательная касается окружности с центром O_{1}
в точке K
, окружности с центром O_{2}
— в точке L
; внутренняя касательная касается первой окружности в точке M
, а второй — в точке N
; прямые KL
и MN
пересекаются в точке A
.
Заметим, что \angle O_{1}AO_{2}=90^{\circ}
как угол между биссектрисами смежных углов. Обозначим \angle KAO_{1}=\alpha
. Тогда \angle AO_{2}L=\angle KAO_{1}=\alpha
как острые углы с соответственно перпендикулярными сторонами. Поэтому
\angle ALN=\angle AO_{2}L=\alpha=\angle KAO_{1},
значит, NL\parallel AO_{1}
. Аналогично KM\parallel AO_{2}
.
Пусть D_{1}
— точка пересечения AO_{1}
и KM
, D_{2}
— точка пересечения AO_{2}
и NL
, а P_{1}
и P_{2}
— точки пересечения прямой O_{1}O_{2}
с прямыми KM
и NL
соответственно. Докажем, что точки P_{1}
и P_{2}
совпадают. Для этого достаточно доказать, что O_{2}P_{1}:P_{1}O_{1}=O_{2}P_{2}:P_{2}O_{1}
.
Из параллельности прямых AO_{1}
и D_{2}P_{2}
следует, что O_{2}P_{2}:P_{2}O_{1}=O_{2}D_{2}:D_{2}A
, а из параллельности прямых D_{1}P_{1}
и AO_{2}
и подобия прямоугольных треугольников AKO_{1}
и O_{2}LA
— O_{2}P_{1}:P_{1}O_{1}=AD_{1}:D_{1}O_{1}=O_{2}D_{2}:D_{2}A
. Что и требовалось доказать.
Источник: Кюршак Й. и др. Венгерские математические олимпиады. — М.: Мир, 1976. — № 183, с. 38
Источник: Венгерские математические олимпиады. — 1961, задача 3
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 1.66, с. 17
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.67, с. 18; № 3.70, с. 64
