1084. Диагонали AC
и BD
выпуклого четырёхугольника ABCD
пересекаются в точке O
. Докажите, что площадь четырёхугольника с вершинами в серединах диагоналей и серединах противоположных сторон AB
и CD
равна полуразности площадей треугольников COD
и AOB
.
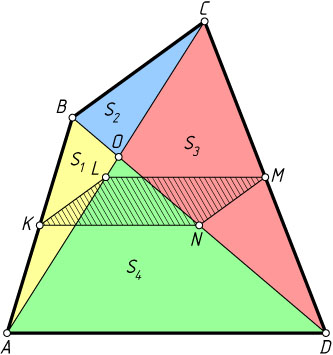
Решение. Пусть K
, L
, M
и N
— середины отрезков AB
, AC
, CD
и BD
соответственно. Обозначим
S_{\triangle AOB}=S_{1},~S_{\triangle BOC}=S_{2},~S_{\triangle COD}=S_{3},~S_{\triangle AOD}=S_{4}.
Тогда S_{ABCD}=S_{1}+S_{2}+S_{3}+S_{4}
. Предположим, что S_{3}\geqslant S_{1}
.
Отрезки ML
и KL
— средние линии треугольников ACD
и ABC
, поэтому
S_{\triangle CML}=\frac{1}{4}S_{\triangle ACD}=\frac{1}{4}(S_{3}+S_{4}),
S_{BKLC}=\frac{3}{4}S_{\triangle ABC}=\frac{3}{4}(S_{1}+S_{2}).
Аналогично
S_{\triangle DMN}=\frac{1}{4}S_{\triangle BCD}=\frac{1}{4}(S_{2}+S_{3}),
S_{AKND}=\frac{3}{4}S_{\triangle ABD}=\frac{3}{4}(S_{1}+S_{4}).
Следовательно,
S_{KLMN}=S_{ABCD}-(S_{\triangle CML}+S_{BKLC}+S_{\triangle DMN}+S_{AKND})=
=S_{1}+S_{2}+S_{3}+S_{4}-\left(\frac{1}{4}(S_{3}+S_{4})+\frac{3}{4}(S_{1}+S_{2})+\frac{1}{4}(S_{2}+S_{3})+\frac{3}{4}(S_{1}+S_{4})\right)=
=S_{1}+S_{2}+S_{3}+S_{4}-\left(\frac{3}{2}S_{1}+S_{2}+\frac{1}{2}S_{3}+S_{4}\right)=\frac{1}{2}S_{3}-\frac{1}{2}S_{1}=\frac{1}{2}(S_{3}-S_{1}).
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 12.16, с. 94
