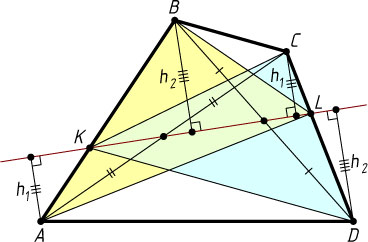
1085. Прямая, проходящая через середины диагоналей AC
и BD
четырёхугольника ABCD
, пересекает стороны AB
и CD
в точках K
и L
соответственно. Докажите, что треугольники ABL
и CDK
равновелики.
Решение. Прямая KL
проходит через середину отрезка AC
, поэтому точки A
и C
равноудалены от этой прямой. Значит, высоты треугольников AKL
и CKL
, опущенные на общую сторону KL
, равны между собой. Обозначим их через h_{1}
. Аналогично равны высоты треугольников BKL
и DKL
, опущенные на общую сторону KL
. Обозначим их через h_{2}
. Тогда
S_{\triangle ABL}=S_{\triangle AKL}+S_{\triangle BKL}=\frac{1}{2}KL\cdot h_{1}+\frac{1}{2}KL\cdot h_{2}=\frac{1}{2}KL(h_{1}+h_{2}),
S_{\triangle CDK}=S_{\triangle CKL}+S_{\triangle DKL}=\frac{1}{2}KL\cdot h_{1}+\frac{1}{2}KL\cdot h_{2}=\frac{1}{2}KL(h_{1}+h_{2}).
Следовательно, S_{\triangle ABL}=S_{\triangle CDK}
.
