10857. Дана трапеция ABCD
с основаниями AD
и BC
. Точки M
и N
— середины AB
и CD
соответственно. Окружность, проходящая через точки B
и C
, пересекает отрезки BM
и CN
в точках P
и Q
(отличных от концов отрезков) соответственно.
а) Докажите, что точки M
, N
, P
и Q
лежат на одной окружности.
б) Найдите QN
, если отрезки DP
и PC
перпендикулярны, AB=21
, BC=4
, CD=20
, AD=17
.
Ответ. \frac{336}{65}
.
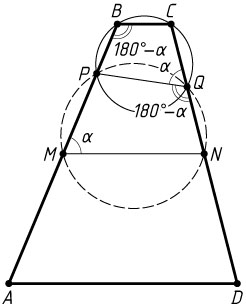
Решение. а) Обозначим \angle BMN=\alpha
. Тогда \angle CBM=180^{\circ}-\alpha
, а так как четырёхугольник BCQP
вписанный, то
\angle CQP=180^{\circ}-\angle CBP=180^{\circ}-\angle CBM=
=180^{\circ}-(180^{\circ}-\alpha)=\alpha=\angle BMN=180^{\circ}-\angle PQN.
Значит, четырёхугольник MPQN
тоже вписанный. Следовательно, точки M
, N
, P
и Q
лежат на одной окружности.
б) Вписанные углы PBQ
и PCQ
опираются на одну и ту же дугу, поэтому
\angle ABQ=\angle PBQ=\angle PCQ=\angle PCD.
Аналогично предыдущему докажем, что четырёхугольник APQD
вписанный, поэтому
\angle BAQ=\angle PAQ=\angle PDQ=\angle PDC,
а так как \angle PDC+\angle PCD=90^{\circ}
, то \angle BAQ+\angle ABQ=90^{\circ}
. Значит, треугольник ABQ
также прямоугольный. Тогда его медиана QM
, проведённая из вершины прямого угла, равна половине гипотенузы AB
, т. е.
QM=\frac{1}{2}AB=\frac{21}{2}.
Кроме того, по теореме о средней линии трапеции
MN=\frac{1}{2}(BC+AD)=\frac{4+17}{2}=\frac{21}{2}=QM,
т. е. треугольник QMN
равнобедренный с боковыми сторонами MQ=MN=\frac{21}{2}
. Тогда
QN=2MN\cos\angle QNM=2MN\cos\angle ADC.
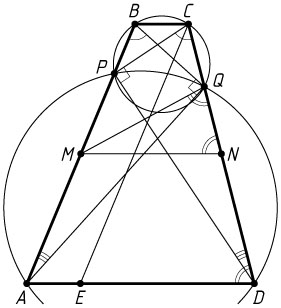
Пусть прямая, проведённая через вершину C
параллельно AB
, пересекает основание AD
в точке E
. Тогда
CE=AB=21,~DE=AD-AE=AD-BC=17-4=13.
По теореме косинусов из треугольника CDE
находим, что
\cos\angle CDE=\frac{DC^{2}+DE^{2}-CE^{2}}{2DC\cdot DE}=\frac{400+169-441}{2\cdot20\cdot13}=\frac{16}{65}.
Следовательно,
QN=2MN\cos\angle ADC=2MN\cos\angle CDE=21\cdot\frac{16}{65}=\frac{336}{65}.
Источник: ЕГЭ. — 2019, 29 марта, досрочный экзамен, № 16

