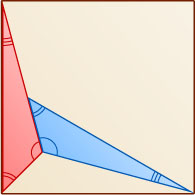
10863. Два равных треугольника расположены внутри квадрата, как показано на рисунке. Найдите их углы.
Ответ. 120^{\circ}
, 45^{\circ}
, 15^{\circ}
.
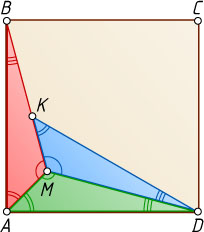
Решение. Заметим, что треугольник MAD
тоже равен треугольнику MAB
— по трём сторонам: сторона MA
у них общая, AD=AB
как стороны квадрата, MD=MB
по условию (лежат напротив соответственных углов в равных треугольниках). Значит,
\angle BAM=\angle MAD=\frac{90^{\circ}}{2}=45^{\circ}.
В точке M
сходятся три соответственных угла равных треугольников, поэтому
\angle AMB=\frac{360^{\circ}}{3}=120^{\circ}.
Сумма углов треугольника равна 180^{\circ}
, значит,
\angle ABM=180^{\circ}-120^{\circ}-45^{\circ}=15^{\circ}.
Автор: Бакаев Е. В.
Источник: Московская математическая олимпиада. — 2019, LXXXII, 7 класс

