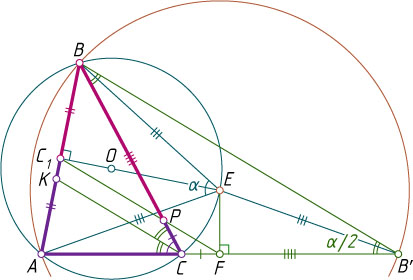
1090. Точка E
— середина той дуги AB
описанной окружности треугольника ABC
, на которой лежит точка C
; C_{1}
— середина стороны AB
. Из точки E
опущен перпендикуляр EF
на прямую AC
. Докажите, что:
а) прямая C_{1}F
делит пополам периметр треугольника ABC
;
б) три такие прямые, построенные для каждой стороны треугольника, пересекаются в одной точке.
Указание. а) На продолжении стороны AC
за точку C
отложите отрезок CB'=AC
. Докажите, что E
— центр окружности, описанной около треугольника ABB'
.
б) Три прямые, о которых говорится в условии задачи, содержат биссектрисы треугольника с вершинами в серединах сторон треугольника ABC
.
Решение. а) На продолжении стороны AC
за точку C
отложим отрезок CB'=CB
. Тогда периметр треугольника ABC
равен сумме отрезков AB
и AB'
. Точка E
— середина дуги AB
, поэтому треугольник AEB
равнобедренный, EA=BE
, а \angle ACB=\angle AEB
, так как вписанные углы ACB
и AEB
опираются на одну и ту же дугу.
Поскольку ACB
— внешний угол равнобедренного треугольника BCB'
, то \angle AB'B=\frac{1}{2}\angle ACB=\frac{1}{2}\angle AEB
. Следовательно, E
— центр окружности, описанной около треугольника ABB'
. Перпендикуляр, опущенный из точки E
на хорду AB'
этой окружности проходит через середину хорды, поэтому F
— середина отрезка AB'
, а C_{1}F
— средняя линия треугольника ABB'
, C_{1}F\parallel BB'
.
Пусть прямая C_{1}F
пересекает сторону BC
в точке P
. Тогда, так как PF\parallel BB'
, то CF=CP
. Следовательно,
AC_{1}+AC+CP=AC_{1}+AC+CF=AC_{1}+AF=\frac{1}{2}AB+\frac{1}{2}AB'=
=\frac{1}{2}(AB+AB')=\frac{1}{2}(AB+AC+CB).
Что и требовалось доказать.
б) Пусть прямая, проходящая через точку C
параллельно BB'
, пересекается с прямой AB
в точке K
. Тогда
\angle ACK=\angle CB'B=\angle CBB'=\angle BCK,
поэтому CK
— биссектриса треугольника ABC
, а так как C_{1}F\parallel BB'
, то C_{1}F\parallel CK
. Заметим, что прямая C_{1}F
проходит через середину C_{1}
стороны AB
треугольника ABC
параллельно биссектрисе его угла при вершине C
, значит, эта прямая содержит биссектрису угла при вершине C_{1}
треугольника с вершинами в серединах сторон AB
, AC
и BC
. Аналогично для остальных двух прямых, о которых говорится в условии задачи. Следовательно, все три такие прямые пересекаются в одной точке. Что и требовалось доказать.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.51, с. 110
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.58, с. 107
