10926. Окружность пересекает стороны треугольника в шести точках (см.рисунок).
а) Докажите, что если a=b
и c=d
, то e=f
.
б) Докажите, что если b=c
и d=e
, то f=a
.
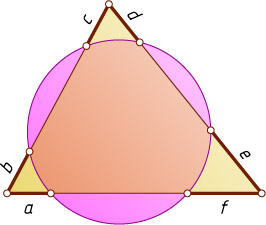
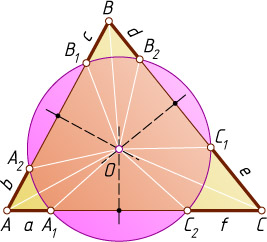
Решение. Введём обозначения, как показано на рисунке.
а) Поскольку a=b
, треугольники OAA_{1}
и OAA_{2}
равны по трём сторонам, а так как c=d
, то равны треугольники OBB_{1}
и OBB_{2}
. Тогда O
— точка пересечения биссектрис углов A
и B
треугольника ABC
, значит, она лежит и на биссектрисе угла C
. Следовательно, стороны угла C
симметричны относительно CO
и окружность симметрична относительно CO
. Тогда треугольники OCC_{1}
и OCC_{2}
симметричны относительно CO
, а значит, и равны. Следовательно, e=f
.
б) Центр O
окружности лежит на серединном перпендикуляре к хорде A_{2}B_{1}
, а так как b=c
, то это и серединный перпендикуляр к AB
. Аналогично, так как d=e
, то точка O
лежит на серединном перпендикуляре к BC
. Тогда O
— точка пересечения серединных перпендикуляров к сторонам AB
и BC
треугольника ABC
, а значит, лежит и на серединном перпендикуляре к стороне AC
. Поскольку A_{1}C_{2}
— хорда окружности, то O
лежит и на серединном перпендикуляре к A_{1}C_{2}
. Следовательно, f=a
.