1094. Третий признак равенства треугольников (по трём сторонам). Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
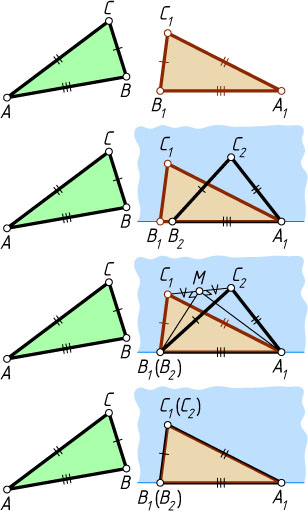
Решение. Пусть ABC
и A_{1}B_{1}C_{1}
— треугольники, у которых AB=A_{1}B_{1}
, BC=B_{1}C_{1}
, AC=A_{1}C_{1}
(рис. 1).
Прямая A_{1}B_{1}
разбивает плоскость на две полуплоскости. Существует треугольник A_{1}B_{2}C_{2}
, равный треугольнику ABC
, с вершиной B_{2}
на луче A_{1}B_{1}
и с вершиной C_{2}
в полуплоскости, содержащей точку C_{1}
(это следует из аксиомы существования треугольника, равного данному: каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данного луча). Поскольку A_{1}B_{1}=AB=A_{1}B_{2}
, вершина B_{2}
совпадает с B_{1}
(по аксиоме откладывания отрезков: на любом луче от его начала можно отложить отрезок заданной длины, и только один).
Если точка C_{2}
совпадает с C_{1}
, то всё доказано. Предположим, что точки C_{1}
и C_{2}
различны. Поскольку A_{1}C_{1}=AC=A_{1}C_{2}
и B_{1}C_{1}=BC=B_{1}C_{2}
, треугольники A_{1}C_{1}C_{2}
и B_{1}C_{1}C_{2}
равнобедренные. Их медианы A_{1}M
и B_{1}M
являются высотами. Значит, из точки M
восставлено два различных перпендикуляра к прямой C_{1}C_{2}
, что невозможно.
Примечание. При доказательстве этого признака мы исходили из такого определения равенства треугольников: треугольники ABC
и A_{1}B_{1}C_{2}
равны, если равны их соответствующие стороны и соответствующие углы, т. е.
AB=A_{1}B_{1},~AC=A_{1}C_{1},~BC=B_{1}C_{1},~\angle A=\angle A_{1},~\angle B=\angle B_{1},~\angle C=\angle C_{1}.
Докажем, что таким образом определяемое равенство треугольников, и равенство, определяемое через их совмещение движением (фигуры называются равными, если существует движение, при котором одна из них переходит в другую), выражают одно и то же.
Действительно, пусть треугольник ABC
совмещается движением с треугольником A_{1}B_{1}C_{1}
, причём вершина A
переходит в вершину A_{1}
, B
— в B_{1}
, C
— в C_{1}
. При движении сохраняются расстояния и величины углов, поэтому
AB=A_{1}B_{1},~AC=A_{1}C_{1},~BC=B_{1}C_{1},~\angle A=\angle A_{1},~\angle B=\angle B_{1},~\angle C=\angle C_{1}.
Обратно, пусть
AB=A_{1}B_{1},~AC=A_{1}C_{1},~BC=B_{1}C_{1},~\angle A=\angle A_{1},~\angle B=\angle B_{1},~\angle C=\angle C_{1}.
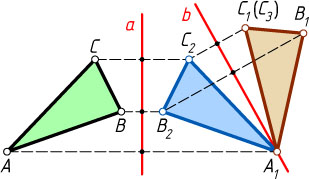
При симметрии относительно серединного перпендикуляра a
к отрезку AA_{1}
треугольник ABC
переходит в равный ему треугольник A_{1}B_{2}C_{2}
. Предположим, что точки B_{1}
и B_{2}
различны. При симметрии относительно серединного перпендикуляра b
к отрезку B_{1}B_{2}
треугольник A_{1}B_{2}C_{2}
переходит в равный ему треугольник A_{1}B_{1}C_{3}
.
Если точки C_{1}
и C_{3}
лежат по одну сторону от прямой A_{1}B_{1}
, то они совпадают (рис. 3). Действительно, поскольку углы B_{1}A_{1}C_{1}
и B_{1}A_{1}C_{3}
равны, то лучи A_{1}C_{1}
и A_{1}C_{3}
совпадают (аксиома откладывания углов), а так как отрезки A_{1}C_{1}
и A_{1}C_{3}
равны, то совпадают точки C_{1}
и C_{3}
(аксиома откладывания отрезков). Таким образом, треугольник ABC
движением переведён в треугольник A_{1}B_{1}C_{1}
.
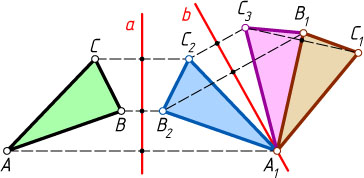
Если же точки C_{1}
и C_{3}
лежат по разные стороны от прямой A_{1}B_{1}
(рис. 4), то надо ещё рассмотреть симметрию относительно прямой A_{1}B_{1}
.
Таким образом, треугольник ABC
можно перевести в треугольник A_{1}B_{1}C_{1}
либо с помощью симметрии, либо с помощью композиции двух или трёх симметрий.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 39
Источник: Погорелов А. В. Геометрия: Учебное пособие для 7—11 кл. средней школы. — 8-е изд. — М.: Просвещение, 1989. — с. 40, с. 150


