1095. Признаки равенства прямоугольных треугольников. Прямоугольные треугольники равны:
1) по двум катетам;
2) по катету и прилежащему острому углу;
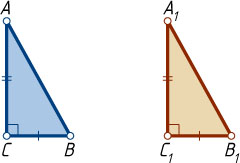
3) по катету и гипотенузе;
4) по гипотенузе и острому углу;
5) по катету и противолежащему острому углу.
Решение. 1) Треугольники равны по двум сторонам и углу между ними.
2) Треугольники равны по стороне и прилежащим к ней углам.
3) Пусть ABC
и A_{1}B_{1}C_{1}
— прямоугольные треугольники, у которых \angle C=\angle C_{1}=90^{\circ}
, AB=A_{1}B_{1}
и BC=B_{1}C_{1}
.
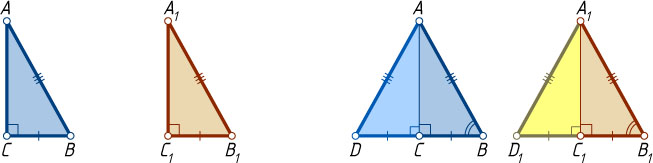
На продолжении катета BC
за точку C
отложим отрезок CD=BC
(по аксиоме откладывания отрезков: на любом луче от его начала можно отложить отрезок заданной длины, и только один). Тогда прямоугольные треугольники ACD
и ACB
равны по двум катетам, поэтому AD=AB
. Аналогично построим точку D_{1}
на продолжении катета B_{1}C_{1}
прямоугольного треугольника A_{1}B_{1}C_{1}
и получим, что A_{1}D_{1}=B_{1}C_{1}
. Тогда BD=2BC=2B_{1}C_{1}=B_{1}D_{1}
.
Три стороны треугольника ABD
соответственно равны трём сторонам треугольника A_{1}B_{1}D_{1}
, поэтому они равны. Значит, \angle B=\angle B_{1}
. Следовательно, треугольники ABC
и A_{1}B_{1}C_{1}
равны по двум сторонам и углу между ними.
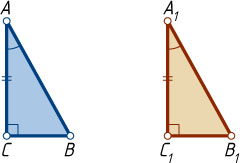
4) Пусть ABC
и A_{1}B_{1}C_{1}
— прямоугольные треугольники, у которых \angle C=\angle C_{1}=90^{\circ}
, AB=A_{1}B_{1}
и \angle BAC=\angle B_{1}A_{1}C_{1}
.
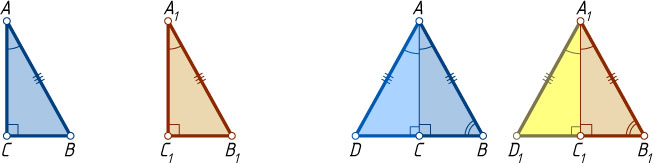
Прямая AC
разбивает плоскость на две полуплоскости. От луча AC
в полуплоскость, не содержащую точку B
, отложим луч под углом, равным углу BAC
(это можно сделать по аксиоме откладывания углов: от любого луча в заданную полуплоскость можно отложить угол с заданной градусной мерой, и только один). На этом луче отложим отрезок AD=AB
(по аксиоме откладывания отрезков: на любом луче от его начала можно отложить отрезок заданной длины, и только один). Тогда треугольник ADC
равен треугольнику ABC
по двум сторонам и углу между ними, поэтому \angle ACD=\angle ACB=90^{\circ}
, а угол BCD
— развёрнутый. Значит, точка C
лежит на стороне BD
треугольника ABD
. Аналогично строится треугольник A_{1}B_{1}D_{1}
.
Поскольку AD=AB=A_{1}B_{1}=A_{1}D_{1}
и \angle BAD=2\angle BAC=2\angle B_{1}A_{1}C_{1}=\angle B_{1}A_{1}D_{1}
, треугольники ABD
и A_{1}B_{1}D_{1}
равны по двум сторонам и углу между ними. Значит, \angle B=\angle ABD=\angle A_{1}B_{1}D_{1}=\angle B_{1}
. Следовательно, треугольники ABC
и A_{1}B_{1}C_{1}
равны по стороне и прилежащим к ней углам.
5) Пусть ABC
и A_{1}B_{1}C_{1}
— прямоугольные треугольники, у которых \angle C=\angle C_{1}=90^{\circ}
, BC=B_{1}C_{1}
и \angle BAC=\angle B_{1}A_{1}C_{1}
.
На продолжении катета AC
за точку C
отложим отрезок CK=A_{1}C_{1}
. Поскольку BC=B_{1}C_{1}
, прямоугольные треугольники BCK
и B_{1}C_{1}A_{1}
равны по двум катетам, поэтому \angle A=\angle A_{1}=\angle K
. Значит, треугольник ABK
равнобедренный, значит, A_{1}B_{1}=BK=AB
. Следовательно, прямоугольные треугольники ABC
и A_{1}B_{1}C_{1}
равны по катету и гипотенузе.

Примечание. В приведённых доказательствах не используется аксиома параллельных.




