10981. Высота BH
треугольника ABC
, опущенная из вершины B
, вторично пересекает окружность, описанную около треугольника ABC
, в точке K
; BN
— диаметр окружности.
а) Докажите, что AN=KC
.
б) Найдите NK
, если радиус окружности равен 20, \angle BAC=25^{\circ}
, \angle BCA=85^{\circ}
.
Ответ. 20\sqrt{3}
.
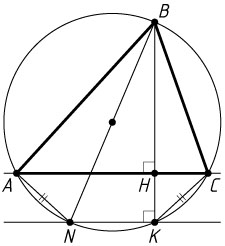
Решение. а) Рассмотрим случай, изображённый на рисунке. Точка K
лежит на окружности с диаметром BN
, поэтому \angle BKN=90^{\circ}
. Прямые NK
и AC
перпендикулярны одной и то же прямой BK
, значит, они параллельны. Дуги AN
и KC
, заключённые между параллельными хордами, равны, поэтому равны хорды AN
и KC
, стягивающие эти дуги. Аналогично для любого другого случая.
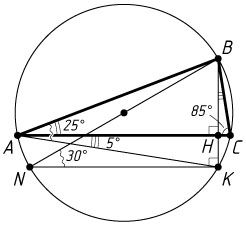
б) Вписанные углы CBK
и CAK
опираются на одну и ту же дугу, поэтому
\angle CAK=\angle CBK=\angle CBH=90^{\circ}-\angle ACB=90^{\circ}-85^{\circ}=5^{\circ}.
Тогда
\angle BNK=\angle BAK=\angle BAC+\angle CAK=25^{\circ}+5^{\circ}=30^{\circ}.
Из прямоугольного треугольника KBN
находим, что
NK=BN\cos\angle BNK=40\cdot\frac{\sqrt{3}}{2}=20\sqrt{3}.
Источник: ЕГЭ. — 2019, 29 мая, задача 16

