10982. Точка O
— центр вписанной в треугольник ABC
окружности. Прямая BO
вторично пересекает описанную около этого треугольника окружность в точке P
.
а) Докажите, что \angle POA=\angle PAO
.
б) Найдите площадь треугольника APO
, если радиус описанной около треугольника ABC
окружности равен 10, \angle BAC=75^{\circ}
, \angle ABC=60^{\circ}
.
Ответ. 25\sqrt{2}
.
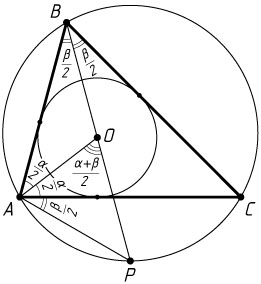
Решение. а) Обозначим углы при вершинах A
и B
треугольника ABC
через \alpha
и \beta
соответственно. Поскольку O
— точка пересечения биссектрис треугольника,
\angle BAO=\angle CAO=\frac{\alpha}{2},~\angle CAP=\angle CBP=\angle ABP=\frac{\beta}{2}.
По теореме о внешнем угле треугольника
\angle POA=\angle BAO+\angle ABP=\frac{\alpha}{2}+\frac{\beta}{2},
а так как
\angle PAO=\angle CAO+\angle CAP=\frac{\alpha}{2}+\frac{\beta}{2},
то \angle POA=\angle PAO
.
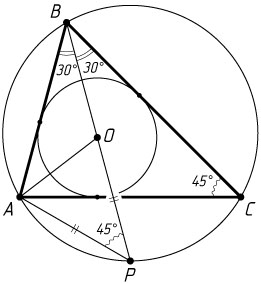
б) Пусть R=10
— радиус окружности, описанной около треугольника ABC
. Треугольник APO
равнобедренный, так как \angle POA=\angle PAO
. Значит,
OP=AP=2R\sin\angle ABP=20\sin30^{\circ}=10,
а так как
\angle APO=\angle APB=\angle ACB=45^{\circ},
то
S_{\triangle APO}=\frac{1}{2}AP\cdot OP\sin\angle APO=\frac{1}{2}\cdot100\sin45^{\circ}=\frac{1}{2}\cdot100\cdot\frac{\sqrt{2}}{2}=25\sqrt{2}.
Источник: ЕГЭ. — 2019, 29 мая, задача 16

