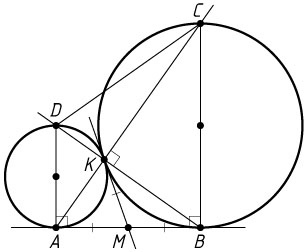
10986. Две окружности разных радиусов касаются внешним образом в точке K
. Прямая касается первой окружности в точке A
, а второй — в точке B
. Луч BK
пересекает первую окружность в точке D
, луч AK
пересекает вторую окружность в точке C
.
а) Докажите, что четырёхугольник ABCD
— трапеция.
б) Найдите радиус окружности, описанной около треугольника BCD
, если радиусы первой и второй окружностей равны соответственно 1 и 4.
Ответ. \frac{\sqrt{65}}{2}
.
Решение. а) Пусть общая касательная к окружностям, проведённая через точку K
, пересекает отрезок AB
в точке M
. Тогда MA=MK=MB
, т. е. медиана KM
треугольника AKB
равна половине стороны AB
. Значит, \angle AKB=90^{\circ}
. Тогда \angle AKD=90^{\circ}
, поэтому AD
— диаметр первой окружности, а так как AB
— касательная, то AD\perp AB
. Аналогично, BC
— диаметр второй окружности, и BC\perp AB
. Значит, AD\parallel BC
. При этом AD\ne BC
. Следовательно, ABCD
— прямоугольная трапеция.
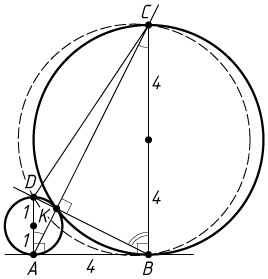
б) Пусть r=1
и R=4
— радиусы окружностей. В прямоугольном треугольнике ABC
известно, что
AB=2\sqrt{rR}=2\sqrt{1\cdot4}=4,
(см. задачу 365) значит,
AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{16+64}=4\sqrt{5}.
Треугольник BKC
подобен треугольнику DKA
с коэффициентом \frac{BC}{AD}=4
, поэтому
CK=\frac{4}{5}\cdot AC=\frac{4}{5}\cdot4\sqrt{5}=\frac{16}{\sqrt{5}}.
Аналогично находим, что DK=\frac{2}{\sqrt{5}}
. Значит,
CD=\sqrt{CK^{2}+DK^{2}}=\sqrt{\left(\frac{16}{\sqrt{5}}\right)^{2}+\left(\frac{2}{\sqrt{5}}\right)^{2}}=\frac{2\sqrt{65}}{\sqrt{5}},
\sin\angle CBD=\sin\angle CBK=\frac{CK}{BC}=\frac{\frac{16}{\sqrt{5}}}{8}=\frac{2}{\sqrt{5}}.
Пусть \rho
— радиус окружности, описанной около треугольника BCD
. Тогда по теореме синусов
\rho=\frac{CD}{2\sin\angle CBD}=\frac{\frac{2\sqrt{65}}{\sqrt{5}}}{2\cdot\frac{2}{\sqrt{5}}}=\frac{\sqrt{65}}{2}.
Источник: ЕГЭ. — 2019, 29 марта, задача 16

