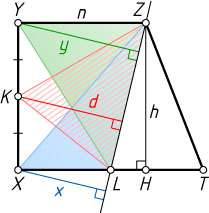
10991. Дана прямоугольная трапеция XYZT
с основаниями XT=m
, YZ=n
и меньшей боковой стороной XY=h
. Точки K
и L
— середины сторон XY
и XT
. Найдите расстояние от точки K
до прямой ZL
.
Ответ. \frac{h(m+2n)}{4\sqrt{h^{2}+\left(\frac{m}{2}-n\right)^{2}}}
.
Решение. Обозначим расстояния от точек X
, Y
и K
до прямой ZL
через x
, y
и d
соответственно. Тогда
d=\frac{x+y}{2}
как средняя линия трапеции с основаниями x
и y
.
Пусть ZH
— высота трапеции. Тогда
ZH=YX=h,~LZ=\sqrt{ZH^{2}+LH^{2}}=\sqrt{h^{2}+\left(\frac{m}{2}-n\right)^{2}}.
Поскольку
x=\frac{2S_{\triangle XLZ}}{LZ}=\frac{\frac{m}{2}\cdot h}{LZ}~\mbox{и}~y=\frac{2S_{\triangle YLZ}}{LZ}=\frac{nh}{LZ},
то
d=\frac{x+y}{2}=\frac{1}{2}\left(\frac{\frac{m}{2}\cdot h}{LZ}+\frac{nh}{LZ}\right)=\frac{h(m+2n)}{4LZ}=\frac{h(m+2n)}{4\sqrt{h^{2}+\left(\frac{m}{2}-n\right)^{2}}}.