10995. Диагонали вписанно-описанного четырёхугольника ABCD
пересекаются в точке T
, а точки I
и O
— центры вписанной и описанной окружностей соответственно. Докажите, что точки O
, I
, T
лежат на одной прямой.
Решение. Лемма 1. Диагонали вписанного в окружность с центром O
четырёхугольника ABCD
пересекаются в точке T
, отличной от O
, стороны AB
и CD
пересекаются в точке P
, а стороны BC
и AD
— в точке Q
. Тогда OT\perp PQ
.
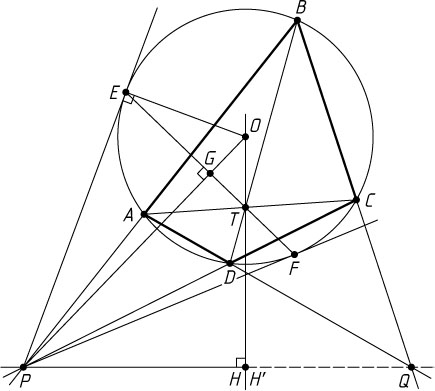
Доказательство. Проведём касательные PE
и PF
к окружности (E
и F
— точки касания), рис. 1. Согласно лемме из решения задачи 1088, прямая EF
проходит через точку T
. Пусть G
— середина хорды EF
, тогда \angle OGT=90^{\circ}
. Опустим перпендикуляр PH
на прямую OT
. Из подобия прямоугольных треугольников OGT
и OHP
получаем OH=\frac{OP\cdot OG}{OT}
. В прямоугольном треугольнике OEP
точка G
— основание высоты, опущенной из вершины прямого угла, значит, OP\cdot OG=OE^{2}=R^{2}
, где R
— радиус окружности. Поэтому OH=\frac{OP\cdot OG}{OT}=\frac{R^{2}}{OT}
. Аналогично, если H'
— основание перпендикуляра, опущенного из точки Q
на прямую OT
, то OH'=\frac{R^{2}}{OT}=OH
, т. е. точки H
и H'
совпадают. Следовательно, PQ\perp OT
. Лемма доказана.
Из доказательства леммы 1 видно, что верна также
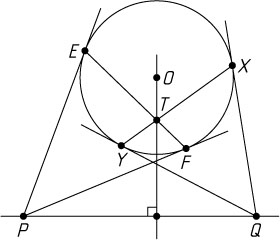
Лемма 2. Если хорды EF
и XY
окружности с центром O
пересекаются в точке T
, отличной от O
, касательные к окружности в точках E
и F
пересекаются в точке P
, а касательные в X
и Y
— в точке Q
, то OT\perp PQ
(рис. 2).
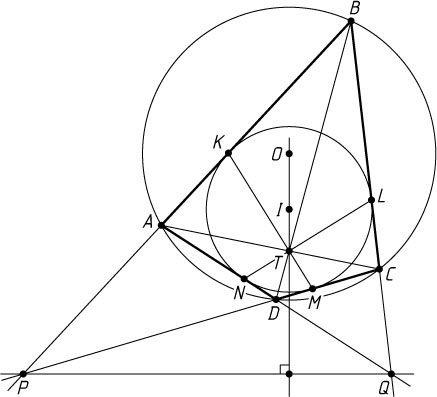
Перейдём к решению нашей задачи. Пусть стороны AB
, BC
, CD
и AD
касаются вписанной окружности в точках K
, L
, M
и N
соответственно; P
— точка пересечения прямых AB
и CD
, Q
— точка пересечения прямых BC
и AD
(рис. 3).
Отрезки KM
и LN
проходят через точку T
(см. задачу 790). Заметим, что P
— точка пересечения касательных ко вписанной окружности в точках K
и M
, а Q
— точка пересечения касательных ко вписанной окружности в точках L
и N
, причём хорды KM
и LN
вписанной окружности пересекаются в точке T
. Из леммы 2 следует, что IT\perp PQ
. Кроме того, по лемме 1 ещё и OT\perp PQ
. Но через точку T
можно провести единственную прямую, перпендикулярную PQ
. Поэтому точки O
, I
и T
лежат на одной прямой.
