1108. Найдите сумму углов при вершинах самопересекающейся пятиконечной звезды.
Ответ. 180^{\circ}
.
Указание. Примените теорему о внешнем угле треугольника.
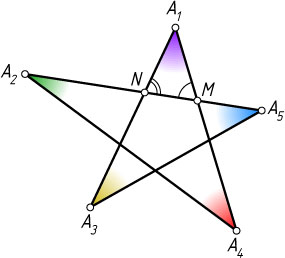
Решение. Первый способ. Обозначим вершины звезды последовательно: A_{1}
, A_{2}
, A_{3}
, A_{4}
, A_{5}
. Пусть M
— точка пересечения отрезков A_{1}A_{4}
и A_{2}A_{5}
, а N
— отрезков A_{1}A_{3}
и A_{2}A_{5}
. Тогда \angle A_{1}MN
— внешний угол треугольника MA_{2}A_{4}
, а \angle A_{1}NM
— внешний угол треугольника NA_{3}A_{5}
. Поэтому
\angle A_{1}MN=\angle A_{2}+\angle A_{4},~\angle A_{1}NM=\angle A_{3}+\angle A_{5}.
Следовательно,
\angle A_{1}+\angle A_{2}+\angle A_{3}+\angle A_{4}+\angle A_{5}=\angle A_{1}+\angle A_{1}MN+\angle A_{1}NM=180^{\circ}.
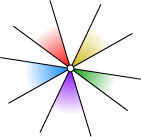
Второй способ. Через произвольную точку проведём 5 прямых, соответственно параллельных сторонам звезды. При этом образуется 10 углов, сумма которых равна 360^{\circ}
. Эта сумма вдвое больше искомой, так как каждый из углов при вершинах звезды соответственно равен двум вертикальным углам из полученных десяти.
Источник: Всероссийская олимпиада школьников. — 1982-83, IX, III этап, 9 класс


