1109. Докажите, что в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине.
Указание. Отложите на продолжении указанной медианы вне треугольника отрезок, равный медиане.
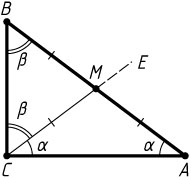
Решение. Первый способ. Пусть ABC
— прямоугольный треугольник с гипотенузой AB
. Обозначим \angle A=\alpha
, \angle B=\beta
. Отложим от луча CA
в полуплоскости, содержащей точку B
, луч под углом \alpha
к CA
. Пусть M
— точка пересечения отложенного луча с гипотенузой AB
. Тогда
\angle BCM=90^{\circ}-\angle ACM=90^{\circ}-\alpha=\beta.
Поэтому треугольники BMC
и AMC
— равнобедренные. Значит,
AM=CM=BM.
Следовательно, CM
— медиана и CM=\frac{1}{2}AB
.
Второй способ. Пусть CM
— медиана прямоугольного треугольника ABC
, проведённая к гипотенузе AB
. Отложим на продолжении этой медианы за точку M
отрезок MP
, равный MC
, и обозначим \angle CAB=\alpha
. Из равенства треугольников PMB
и CMA
(по двум сторонам и углу между ними) следует, что \angle MBP=\alpha
. Поэтому
\angle PBC=\angle PBM+\angle MBC=\alpha+90^{\circ}-\alpha=90^{\circ}.
Следовательно, треугольник PBC
равен треугольнику ACB
(по двум катетам). Поэтому
AB=PC=2CM,~CM=\frac{1}{2}AB.
Третий способ. Центр окружности, описанной около прямоугольного треугольника, совпадает с серединой гипотенузы. Поэтому
MC=MA=MB.
Следовательно, MC=\frac{1}{2}AB
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 42, с. 17
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 7
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 4а, с. 30
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.19, с. 103
