1117. Биссектрисы углов A
и B
треугольника ABC
одинаково наклонены к сторонам BC
и AC
. Найдите зависимость между углами A
и B
.
Ответ. \angle A=\angle B
или \angle A+\angle B=120^{\circ}
.
Указание. Рассмотрите два случая. Воспользуйтесь теоремой о внешнем угле треугольника.
Решение. Пусть AK
и BM
— биссектрисы треугольника ABC
, P
— точка их пересечения. Обозначим \angle A=\alpha
, \angle B=\beta
.
Из условия задачи следует, что \angle AKC=\angle BMC
или \angle AKC+\angle BMC=180^{\circ}
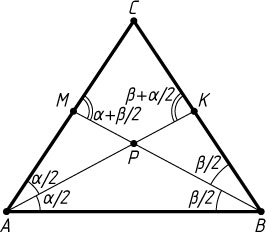
. В первом случае (рис. 1)
\angle AKC=\angle KAB+\angle KBA=\frac{\alpha}{2}+\beta,
\angle BMC=\angle MBA+\angle MAB=\alpha+\frac{\beta}{2}.
Тогда
\frac{\alpha}{2}+\beta=\alpha+\frac{\beta}{2}.
Следовательно, \alpha=\beta
.
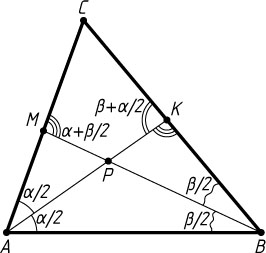
Во втором случае (рис. 2) аналогично получим, что \alpha+\beta=120^{\circ}
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.347, с. 182

