1118. В треугольнике ABC
угол B
равен 36^{\circ}
, угол C
равен 42^{\circ}
. На стороне BC
взята точка M
так, что BM=R
, где R
— радиус окружности, описанной около треугольника ABC
. Найдите угол MAC
.
Ответ. 54^{\circ}
.
Указание. Пусть M_{1}
— точка пересечения стороны BC
с радиусом OA
. Докажите, что M_{1}
совпадает с точкой M
.
Решение. Пусть O
— центр окружности, описанной около треугольника ABC
, M_{1}
— точка пересечения OA
и BC
. Докажем, что M_{1}
совпадает с точкой M
. Действительно,
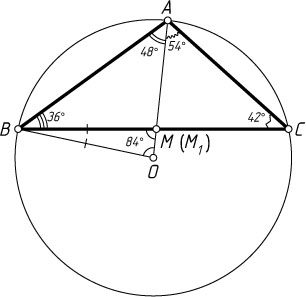
\angle AOB=2\angle BCA=84^{\circ},~\angle OAB=\angle OBA=90^{\circ}-42^{\circ}=48^{\circ},
\angle OM_{1}B=\angle ABC+\angle OAB=36^{\circ}+48^{\circ}=84^{\circ}.
Следовательно, треугольник OBM_{1}
— равнобедренный, BM_{1}=BO=R
. Поэтому точки M_{1}
и M
совпадают. Тогда
\angle MAC=\angle BAC-\angle BAM=102^{\circ}-48^{\circ}=54^{\circ}.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 691, с. 87
