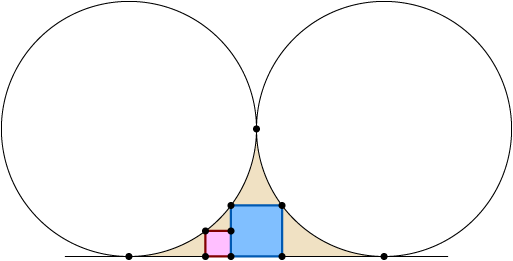
11187. В криволинейный треугольник, ограниченный двумя дугами равных касающихся окружностей и их общей касательной, помещены синий и красный квадраты, как показано на рисунке. Докажите, что сторона синего квадрата вдвое больше стороны красного.
Решение. Первый способ. Пусть O_{1}
и O_{2}
— центры равных касающихся окружностей радиуса R
, A
и B
— их общая касательная (точка A
лежит на первой окружности, B
— на второй), C
— точка касания окружностей, D
— точка пересечения AB
и общей касательной окружностей, проведённой через точку C
, KLMN
— синий квадрат (точки K
и L
лежат на отрезке AB
, точка N
лежит на первой окружности, M
— на второй), P
— точка пересечения CD
и MN
, Q
— середина PD
(рис. 1).
При симметрии относительно прямой DO_{2}
точка M
переходит в точку F
, лежащую на второй окружности, прямоугольник DLMP
— в равный ему прямоугольник DGFQ
, точка G
— на отрезке BD
. При этом симметричные отрезки ML
и FQ
пересекаются в точке E
, лежащей на оси симметрии. Значит,
GF=PM=\frac{1}{2}ML,~LG=PQ=\frac{1}{2}DP=\frac{1}{2}ML.
Значит, LGFE
— квадрат, а из единственности следует, что LGFE
— красный квадрат, и его сторона вдвое меньше стороны квадрата KLMN
.
Второй способ. Пусть O_{1}
и O_{2}
— центры равных касающихся окружностей радиуса R
, A
и B
— их общая касательная (точка A
лежит на первой окружности, B
— на второй), KLMN
— синий квадрат (точки K
и L
лежат на отрезке AB
, точка N
лежит на первой окружности, M
— на второй), EFGL
— красный квадрат (точка K
лежит на отрезке ML
, точка F
— на второй окружности, точка G
— на отрезке BL
, рис. 2.).
Пусть X
— проекция точки N
на радиус O_{1}A
, Y
— проекция точки F
на радиус O_{2}B
. Обозначим через R
радиусы окружностей, x
и y
— стороны синего и красного квадратов соответственно. Из прямоугольного треугольника O_{1}XN
получаем, что
O_{1}X^{2}+NX^{2}=O_{1}P^{2},~\mbox{или}~(R-x)^{2}+\left(R-\frac{x}{2}\right)^{2}=R^{2}.
Из этого уравнения находим, что x=\frac{2}{5}R
.
Из прямоугольного треугольника O_{2}YF
получаем, что
O_{2}Y^{2}+FY^{2}=O_{2}F^{2}~\mbox{или}~(R-y)^{2}+\left(R-y-\frac{x}{2}\right)^{2}=R^{2},
а так как x=\frac{2}{5}R
, то
(R-y)^{2}+\left(\frac{4}{5}R-y\right)^{2}=R^{2},
откуда y=\frac{1}{5}R
. Следовательно, y=2x
.
Автор: Произволов В. В.
Источник: Журнал «Квант». — 2004, № 2, с. 15, М1901; 2004, № 5, с. 21, М1901
Источник: Задачник «Кванта». — 2004, № 2, М1901
