1119. Один из углов треугольника равен 120^{\circ}
. Докажите, что треугольник, образованный основаниями биссектрис данного, — прямоугольный.
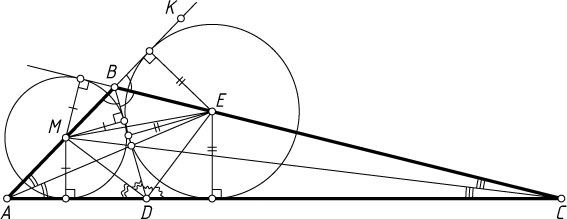
Указание. Пусть AE
и BD
— биссектрисы треугольника ABC
и \angle ABC=120^{\circ}
. Тогда BE
— биссектриса угла DBK
, смежного с углом ABD
.
Решение. Пусть AE
, BD
и CM
— биссектрисы треугольника ABC
и \angle ABC=120^{\circ}
. На продолжении стороны AB
за точку B
возьмём точку K
. Поскольку
\angle EBK=180^{\circ}-\angle ABC=180^{\circ}-120^{\circ}=60^{\circ}=\angle DBE,
то BE
— биссектриса угла DBK
, смежного с углом ABD
. Поэтому точка E
равноудалена от прямых AB
и DB
, а так как точка E
лежит на биссектрисе угла BAC
, то она равноудалена от прямых AB
и CD
. Поэтому точка E
равноудалена от сторон угла BDC
. Значит, DE
— биссектриса угла BDC
. Аналогично DM
— биссектриса угла ADB
. Следовательно,
\angle MDE=\frac{1}{2}(\angle ADB+\angle BDC)=\frac{1}{2}\cdot180^{\circ}=90^{\circ}.
Примечание. Верно и обратное: если AE
, BD
и CM
— биссектрисы треугольника ABC
и \angle MDE=90^{\circ}
, то \angle ABC=120^{\circ}
(см. задачу 4116).
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 170, с. 195
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 258, с. 31
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 258, с. 29
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.35, с. 105
Источник: Олимпиада «Шаг в будущее». — 2019, 10 класс, № 4, вариант 1
Источник: Кушнир И. А. Геометрия. Поиск и вдохновение. — М.: МЦНМО, 2013. — с. 488
