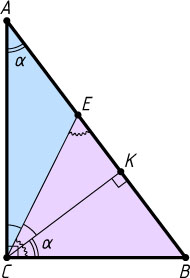
1120. В прямоугольном треугольнике ABC
проведена высота CK
из вершины прямого угла C
, а в треугольнике ACK
— биссектриса CE
. Докажите, что CB=BE
.
Указание. Выразите углы треугольника CBE
через \angle A
.
Решение. Обозначим \angle A=\alpha
. Тогда
\angle ACK=90^{\circ}-\alpha,~\angle ECK=\angle ACE=\frac{90^{\circ}-\alpha}{2}=45^{\circ}-\frac{\alpha}{2},
\angle KCB=\alpha,~\angle CEB=\angle A+\angle ACE=\alpha+45^{\circ}-\frac{\alpha}{2}=45^{\circ}+\frac{\alpha}{2},
\angle BCE=\angle KCB+\angle ECK=\alpha+45^{\circ}-\frac{\alpha}{2}=45^{\circ}+\frac{\alpha}{2}.
Следовательно, треугольник CBE
равнобедренный и CB=BE
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.20, с. 107
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.25, с. 104
