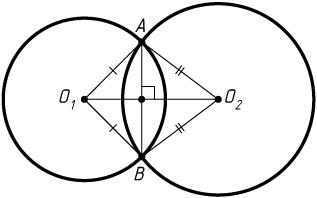
1130. Две окружности пересекаются в точках A
и B
. Докажите, что прямая, проходящая через центры окружностей, делит отрезок AB
пополам и перпендикулярна ему.
Указание. Воспользуйтесь свойством серединного перпендикуляра к отрезку.
Решение. Центры O_{1}
и O_{2}
окружностей равноудалены от точек A
и B
, следовательно, O_{1}O_{2}
— серединный перпендикуляр к отрезку AB
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 73
