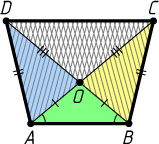
1133. Диагонали AC
и BD
четырёхугольника ABCD
пересекаются в точке O
. Периметр треугольника ABC
равен периметру треугольника ABD
, а периметр треугольника ACD
— периметру треугольника BCD
. Докажите, что AO=BO
.
Указание. Сложите и вычтите равенства
BC+AC=BD+AD~\mbox{и}~BC+BD=AC+AD.
Решение. Из условия задачи следует, что
BC+AC=BD+AD~\mbox{и}~BC+BD=AC+AD.
Складывая и вычитая эти равенства, получим, что BC=AD
и AC=BD
. Значит, треугольники ABC
и BAD
равны по трём сторонам, поэтому \angle BAC=\angle ABD
, треугольник AOB
равнобедренный. Следовательно, AO=BO
.