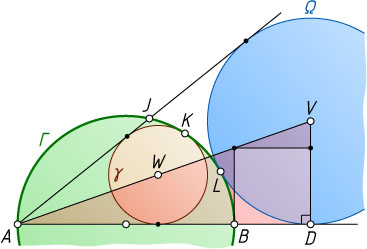
11333. Точка J
лежит на окружности \Gamma
с диаметром AB
(см. рис.). Окружность \gamma
с центром W
, вписанная в криволинейный треугольник ABJ
, касается окружности \Gamma
в точке K
. Окружность \Omega
с центром V
, вписанная в угол BAJ
, касается внешним образом окружности \Gamma
в точке L
.
а) Если меньшие дуги KL
и BL
окружности \Gamma
равны, то какова их градусная мера?
б) Докажите, что отрезок BD
равен стороне вписанного в треугольник ADV
квадрата, с общим прямым углом при вершине D
.
Ответ. а) 30^{\circ}
.
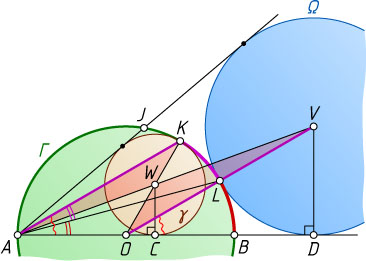
Решение. а) Пусть O
— центр окружности \Gamma
. Дуги KL
и LB
равны, поэтому равны опирающиеся на них вписанные в окружность \Gamma
углы KAL
и BAL
. Значит,
\angle KAB=\frac{1}{2}\smile BLK=\frac{1}{2}\angle BOK=\angle BOL.
Следовательно, AK\parallel OL
, а так как точка L
лежит на прямой OV
, то AK\parallel OV
.
Треугольники AWK
и VWO
подобны, поэтому \frac{AW}{WV}=\frac{WK}{OW}
. Также подобны и прямоугольные треугольники ACW
и ADV
, поэтому
\frac{AW}{WV}=\frac{AW}{AV-AW}=\frac{WC}{DV-WC}=\frac{WK}{DV-WK}.
Значит,
DV-WK=OW,~\mbox{или}~DV=OW+WK=OK,
т. е. равны радиусы окружностей \Gamma
и \Omega
.
Тогда
\frac{DV}{OV}=\frac{DV}{OL+LV}=\frac{DV}{2DV}=\frac{1}{2}.
Следовательно,
\smile KL=\smile BL=\angle BOL=\angle DOV=30^{\circ}.
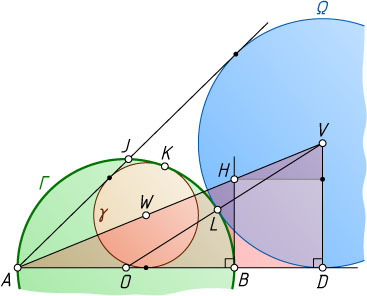
б) Через точку B
перпендикулярно AD
проведём прямую, пересекающую AV
в точке H
. По теореме Пифагора
OD^{2}+DV^{2}=OV^{2}~\Leftrightarrow~(OB+BD)^{2}+DV^{2}=(OL+LV)^{2}~\Leftrightarrow
\Leftrightarrow~OB^{2}+2OB\cdot BD+BD^{2}+DV^{2}=OL^{2}+2OL\cdot LV+LV^{2}~\Leftrightarrow
\Leftrightarrow~2OB\cdot BD+BD^{2}+DV^{2}=2OL\cdot LV+LV^{2}~\Leftrightarrow
\Leftrightarrow~BD(2OB+BD^{2})=2OL\cdot LV~\Leftrightarrow~BD(2OB+BD)=AB\cdot DV,
откуда
\frac{BD}{AB}=\frac{DV}{2OB+BD}=\frac{DV}{AB+BD}=\frac{DV}{AD},
а так как \frac{BH}{AB}=\frac{DV}{AD}
(из подобия прямоугольных треугольников ABH
и ADV
), то \frac{BH}{AB}=\frac{BD}{AB}
. Следовательно, BH=BD
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1985, № 6, задача 934 (1984, с. 114), с. 194


