11398. Две окружности касаются внутренним образом в точке C
. Вершины A
и B
равнобедренного прямоугольного треугольника ABC
с прямым углом C
лежат на меньшей и большей окружностях соответственно. Прямая AC
вторично пересекает большую окружность в точке E
. Прямая BC
вторично пересекает меньшую окружность в точке D
.
а) Докажите, что AD
параллельно BE
.
б) Найдите AC
, если радиусы окружностей равны 3 и 4.
Ответ. \frac{24}{5}
.
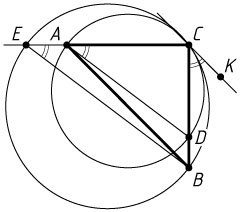
Решение. а) Проведём в точке C
общую касательную к окружностям. Отметим на ней точку K
, лежащую с точкой B
по одну сторону от прямой AC
. Из теоремы об угле между касательной и хордой следует, что
\angle BEC=\angle BCK=\angle DCK=\angle DAC.
Значит, AD\parallel BE
.
б) Поскольку \angle ACD=\angle BCE=90^{\circ}
, отрезки AD
и BE
— диаметры окружностей, поэтому AD=6
и BE=8
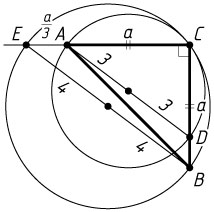
. Обозначим AC=BC=a
, CE=b
. Прямоугольные треугольники ACD
и ECB
подобны с коэффициентом \frac{AD}{BE}=\frac{3}{4}
, значит, \frac{CA}{CE}=\frac{3}{4}
, или \frac{a}{b}=\frac{3}{4}
, откуда b=\frac{4}{3}a
.
По теореме Пифагора из треугольника BCE
получаем, что
a^{2}+b^{2}=64,~\mbox{или}~a^{2}+\frac{16}{9}a^{2}=64,
откуда AC=a=\frac{24}{5}
.
Источник: ЕГЭ. — 2020, июль, задача 16

