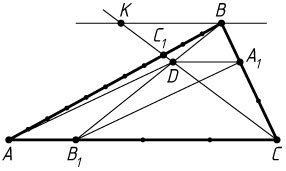
11399. На сторонах AB
, BC
и AC
треугольника ABC
отмечены точки C_{1}
, A_{1}
и B_{1}
соответственно, причём AC_{1}:C_{1}B=8:3
, BA_{1}:A_{1}C=1:2
, CB_{1}:B_{1}A=3:1
. Отрезки BB_{1}
и CC_{1}
пересекаются в точке D
.
а) Докажите, что ADA_{1}B_{1}
— параллелограмм.
б) Найдите CD
, если отрезки AD
и BC
перпендикулярны, AC=28
, BC=18
.
Ответ. 17.
Решение. а) Через точку B
параллельно AC
проведём прямую. Пусть эта прямая пересекается с продолжением CC_{1}
в точке K
. Из подобия треугольников BC_{1}K
и AC_{1}C
получаем, что BK=\frac{3}{8}AC
, а из подобия треугольников BDK
и B_{1}DC
—
\frac{BD}{DB_{1}}=\frac{BK}{CB_{1}}=\frac{\frac{3}{8}AC}{\frac{3}{4}AC}=\frac{1}{2}=\frac{BA_{1}}{A_{1}C}.
Значит, DA_{1}\parallel CB_{1}
, поэтому DA_{1}\parallel AB_{1}
. Кроме того, из подобия треугольников BDA_{1}
и BB_{1}C
получаем, что DA_{1}=\frac{1}{3}B_{1}C=AB_{1}
. Противоположные стороны DA_{1}
и AB_{1}
четырёхугольника ADA_{1}B_{1}
равны и параллельны, следовательно, это параллелограмм.
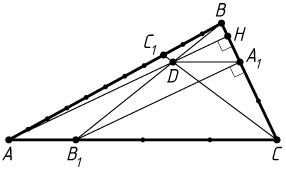
б) Поскольку A_{1}B_{1}\parallel AD
, а AD\perp BC
, то A_{1}B_{1}\perp BC
, т. е. треугольник A_{1}CB_{1}
прямоугольный с прямым углом при вершине A_{1}
. В этом треугольнике известно, что
A_{1}C=\frac{2}{3}BC=12,~B_{1}C=\frac{3}{4}AC=21,~A_{1}B_{1}=\sqrt{21^{2}-12^{2}}=3\sqrt{33}.
Пусть прямая AD
пересекает сторону BC
в точке H
. Из подобия прямоугольных треугольников A_{1}B_{1}C
и HAC
находим, что
AH=\frac{4}{3}A_{1}B_{1}=4\sqrt{33},~CH=\frac{4}{3}CA_{1}=16.
Тогда
DH=AH-AD=AH-A_{1}B_{1}=4\sqrt{33}-3\sqrt{33}=\sqrt{33}.
Следовательно,
CD=\sqrt{CH^{2}+DH^{2}}=\sqrt{16^{2}+33}=\sqrt{289}=17.
Источник: ЕГЭ. — 2020, июль, задача 16

