11400. Дан прямоугольный треугольник ABC
. На катете AC
отмечена точка M
, а на продолжении катета BC
за точку C
— точка N
так, что CM=CB
и CA=CN
.
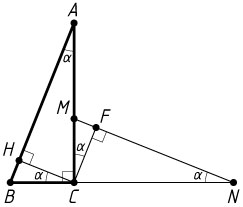
а) Пусть CH
и CF
— высоты треугольников ABC
и NMC
соответственно. Докажите, что CF
и CH
перпендикулярны.
б) Пусть L
— точка пересечения BM
и AN
, BC=2
, AC=5
. Найдите ML
.
Ответ. \frac{3}{\sqrt{2}}
Решение. а) Обозначим \angle BAC=\angle BCH=\alpha
. Прямоугольный треугольник NMC
равен прямоугольному треугольнику ABC
по двум катетам, поэтому \angle MCF=\angle CNM=\alpha
. Следовательно,
\angle FCH=\angle FCM+\angle ACH=\alpha+(90^{\circ}-\alpha)=90^{\circ}.
Что и требовалось доказать.
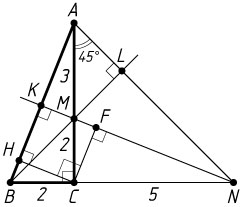
б) Пусть прямые NM
и AB
пересекаются в точке K
, а прямые BM
и AN
— в точке L
. Три угла четырёхугольника CFKH
равны по 90^{\circ}
, значит, четвёртый тоже равен 90^{\circ}
. Тогда NK\perp AB
, поэтому NK
— высота треугольника ABN
, а так как высоты треугольника пересекаются в одной точке, то BL
— третья высота треугольника ABN
.
В равнобедренном прямоугольном треугольнике AML
угол при вершине A
равен 45^{\circ}
, следовательно,
ML=\frac{AM}{\sqrt{2}}=\frac{AC-CM}{\sqrt{2}}=\frac{AC-BC}{\sqrt{2}}=\frac{5-2}{\sqrt{2}}=\frac{3}{\sqrt{2}}.
Источник: ЕГЭ. — 2020, июль, задача 16

