11445. На боковых сторонах AC
и BC
равнобедренного треугольника ABC
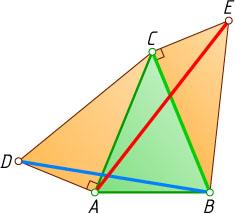
как на катетах построены вовне равные прямоугольные треугольники ADC
и CEB
(см. рис.). Докажите, что из отрезков BD
, AE
и BC
можно сложить треугольник.
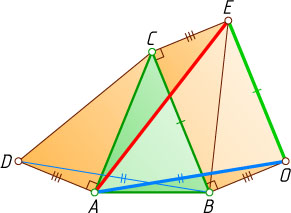
Решение. Достроим треугольник BEC
до прямоугольника ECBO
. Тогда треугольник AEO
— искомый. Действительно, EO=BC
(стороны прямоугольника), а AO=BD
, так как треугольники ABO
и BAD
равны по двум сторонам (AB
— общая, BO=CE=AD
) и углу между ними
(\angle DAB=90^{\circ}+\angle CAB=90^{\circ}+\angle CBA=\angle OBA).
Автор: Пешнин А. М.
Источник: Журнал «Квантик». — 2017, № 10, с. 27, задача 10, 7-8 классы

