11479. В трапеции ABCD
боковая сторона AB
равна диагонали BD
. Точка M
— середина диагонали AC
. Прямая BM
пересекает отрезок CD
в точке E
. Докажите, что BE=CE
.
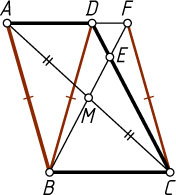
Указание. На луче AD
отложим отрезок AF=BC
. Тогда ABCF
— параллелограмм, а BDFC
— равнобедренная трапеция.
Решение. На луче AD
отложим отрезок AF=BC
. Тогда ABCF
— параллелограмм, а M
— точка пересечения его диагоналей. Тогда CF=AB=BD
, т. е. четырёхугольник BCFD
— равнобедренная трапеция. Точка E
— точка пересечения её диагоналей, следовательно, BE=CE
.
Автор: Кузнецов А. С.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2019, первый тур, задача 3, 8 класс
