11490. Окружности \omega_{1}
и \omega_{2}
пересекаются в точках P
и Q
. Пусть O
— точка пересечения общих внешних касательных \omega_{1}
и \omega_{2}
. Прямая, проходящая через точку O
, пересекает \omega_{1}
и \omega_{2}
в точках A
и B
, как показано на рисунке. Прямая PA
повторно пересекает \omega_{2}
в точке C
, а прямая QB
повторно пересекает \omega_{1}
в точке D
. Докажите, что точки O
, C
и D
лежат на одной прямой.
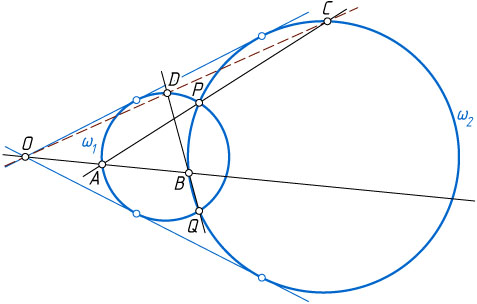
Указание. Примените гомотетию.
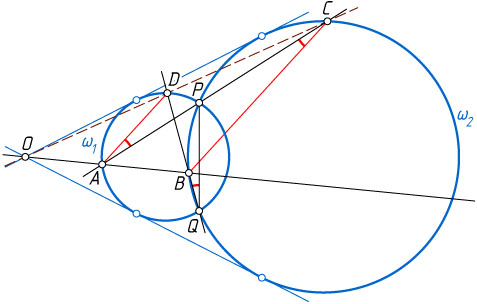
Решение. Из вписанности четырёхугольников ADPQ
и BPCQ
следует, что
\angle DAC=\angle DQP=\angle BCP,
т. е. AD\parallel BC
. Поскольку точка O
— центр гомотетии данных окружностей и точка A
при этой гомотетии переходит в B
, то точка D
переходит в C
. Следовательно, точки O
, C
и D
лежат на одной прямой.
Автор: Акопян А. В.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2020, XVI, заочный тур, 8-9 классы, задача 6

