11634. На каждой стороне треугольника отметили по точке и соединили эти точки отрезками, тем самым разбив треугольник на четыре меньших треугольника. Все четыре оказались подобны друг другу. Обязательно ли эти четыре треугольника равны?
Ответ. Нет, не обязательно.
Решение. Рассмотрим неравнобедренный прямоугольный треугольник ABC
с острым углом \alpha\ne45^{\circ}
при вершине A
. Из вершины C
прямого угла проведём высоту CH
и из точки H
опустим перпендикуляры HD
и HE
на катеты AC
и BC
соответственно. Тогда
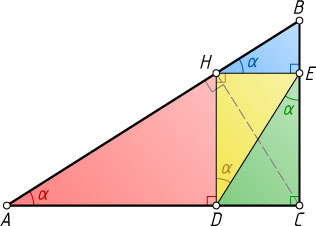
\angle DEC=\angle EDH=\angle ECH=\angle BCH=\angle BHE=\angle HAD=\alpha.
Следовательно, неравные прямоугольные треугольники DCE
, EHD
, BEH
, HDA
подобны по двум углам.
Автор: Шаповалов А. В.
Источник: Грибалко А. В., Медников Л. Э. XXI—XXII турниры математических боёв имени А. П. Савина. — М.: МЦНМО, 2020. — № 290, с. 39
