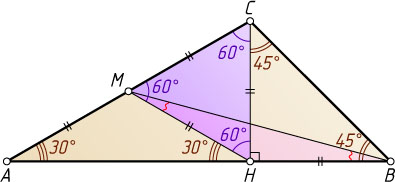
11653. В треугольнике ABC
угол A
равен 30^{\circ}
, а угол C
равен 105^{\circ}
. Найдите угол между медианой BM
и стороной AB
.
Ответ. 15^{\circ}
.
Решение. Проведём высоту CH
треугольника ABC
. В прямоугольном треугольнике BHC
угол при вершине B
равен 45^{\circ}
, значит, этот треугольник равнобедренный, BH=CH
.
В прямоугольном треугольнике AHC
катет CH
лежит против угла в 30^{\circ}
, поэтому
CH=\frac{1}{2}AC=CM.
В равнобедренном треугольнике CMH
угол при вершине C
равен 60^{\circ}
, значит, этот треугольник равносторонний. Тогда
MH=CH=BH,
поэтому треугольник BHM
равнобедренный. Его внешний угол при вершине H
равен 90^{\circ}-60^{\circ}=30^{\circ}
. Следовательно,
\angle ABM=\angle HBM=\frac{1}{2}\angle AHM=15^{\circ}.
Автор: Калинин Д. А.
Источник: Грибалко А. В., Медников Л. Э. XXI—XXII турниры математических боёв имени А. П. Савина. — М.: МЦНМО, 2020. — № 257, с. 35
