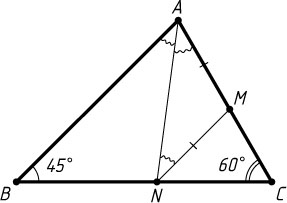
1167. На сторонах AC
и BC
треугольника ABC
взяты соответственно точки M
и N
, причём MN\parallel AB
и MN=AM
. Найдите угол BAN
, если \angle B=45^{\circ}
и \angle C=60^{\circ}
.
Ответ. 37{,}5^{\circ}
.
Указание. AN
— биссектриса треугольника ABC
.
Решение. Треугольник AMN
— равнобедренный, поэтому \angle MAN=\angle MNA
, а так как MN\parallel AB
, то \angle MNA=\angle BAN
, значит \angle CAN=\angle BAN
. Следовательно, AN
— биссектриса угла BAC
. Поскольку
\angle BAC=180^{\circ}-\angle ABC-\angle ACB=75^{\circ},
то
\angle BAN=\frac{1}{2}\angle BAC=37{,}5^{\circ}.