11678. Треугольники AMB
и BNC
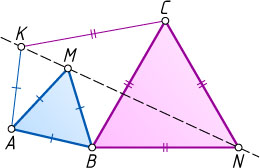
равносторонние (см. рис.), точка K
выбрана так, что AK=AB
и CK=CB
. Докажите, что точки K
, M
и N
лежат на одной прямой.
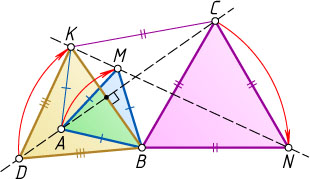
Решение. Первый способ. Построим равносторонний треугольник BKD
так, чтобы точки D
и C
лежали по разные стороны от прямой BK
(см. рис.). Точки C
, A
и D
равноудалены от концов отрезка BK
, значит, они лежат на одной прямой — на серединном перпендикуляре к отрезку BK
.
При повороте вокруг точки B
на 60^{\circ}
по часовой стрелке точки D
, A
и C
, лежащие на одной прямой, перейдут в точки K
, M
и N
соответственно. Следовательно, точки K
, M
и N
тоже лежат на одной прямой.
Второй способ. При повороте вокруг точки B
на 60^{\circ}
по часовой стрелке точки A
и C
переходят в точки M
и N
соответственно. Тогда треугольник ABC
переходит в треугольник MBN
. Значит, эти треугольники равны.
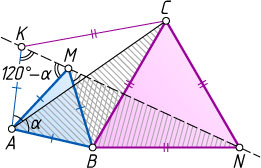
Пусть \angle BAC=\angle BMN=\alpha
. Треугольники ABC
и AKC
тоже равны (по трём сторонам), поэтому
\angle KAB=2\alpha,~\angle KAM=\angle KAB-\angle MAB=2\alpha-60^{\circ}.
Треугольник MAK
равнобедренный, поэтому
\angle KMA=90^{\circ}-\frac{1}{2}\angle KAM=90^{\circ}-\frac{1}{2}(2\alpha-60^{\circ})=120^{\circ}-\alpha.
Значит,
\angle KMA+\angle AMB+\angle BMN=(120^{\circ}-\alpha)+60^{\circ}+\alpha=180^{\circ}.
Следовательно, точки K
, M
и N
лежат на одной прямой.
Автор: Акопян А. В.
Источник: Грибалко А. В., Медников Л. Э. XXI—XXII турниры математических боёв имени А. П. Савина. — М.: МЦНМО, 2020. — № 298, с. 40


